
题目列表(包括答案和解析)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
设集合 ,
,  , 则A∩B=( )
, 则A∩B=( )
A. B.
B. C.
C.
 D.
D.

设集合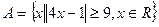 ,
, 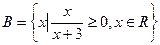 , 则A∩B=( )
, 则A∩B=( )
A.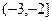 | B. | C.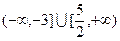 | D.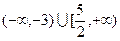 |
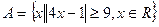 ,
, 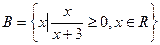 , 则A∩B=( )
, 则A∩B=( ) A.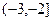 | B. | C.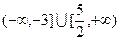 | D.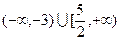 |
设集合 ,
,
 ,
则A∩B=( )
,
则A∩B=( )
A.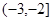 B.
B.
C. D.
D.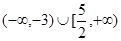
1、D 2、D 3、(理)B(文)4、C 5、C 6、(理)A(文)D 7、C 8、D 9、(理)B(文)A
10、D
二、填空题
11、2 12、(理)1(文)―1 13、96 14、10、32
三、解答题
15、解:(Ⅰ)由 ,得
,得 ,
,
由 ,得
,得 .
.
所以 .??????????????????????????????????????????? 5分
.??????????????????????????????????????????? 5分
(Ⅱ)由 得
得 ,
,
由(Ⅰ)知 ,
,
故 ,??????????????????????????????????????????????????????????????????????????????????????????????????????? 8分
,??????????????????????????????????????????????????????????????????????????????????????????????????????? 8分
又 ,
,
故 ,
, .
.
所以 .????????????????????????????????????????????????????????????????????????????????????? 10分
.????????????????????????????????????????????????????????????????????????????????????? 10分
17、(理)解: (1)  若
若  则
则  列表如下
列表如下






+
0
-
-

单调增
极大值
单调减
单调减
(2) 在  两边取对数, 得
两边取对数, 得  ,由于
,由于 所以
所以
 (1)
(1)
由(1)的结果可知,当 时,
时,  ,
,
为使(1)式对所有 成立,当且仅当
成立,当且仅当 ,即
,即
(文)解:(1)  ,由于函数
,由于函数 在
在 时取得极值,所以
时取得极值,所以 
即 
(2) 方法一:由题设知: 对任意
对任意 都成立
都成立
即 对任意
对任意 都成立
都成立
设  , 则对任意
, 则对任意 ,
, 为单调递增函数
为单调递增函数
所以对任意 ,
, 恒成立的充分必要条件是
恒成立的充分必要条件是
即  ,
,
于是 的取值范围是
的取值范围是
18、解:证明:(Ⅰ)作AD的中点O,则VO⊥底面ABCD.…………………………1分
建立空间直角坐标系,并设正方形边长为1,…………………………2分
则A( ,0,0),B(
,0,0),B( ,1,0),C(-
,1,0),C(- ,1,0),
,1,0),
D(- ,0,0),V(0,0,
,0,0),V(0,0, ),
),
∴ ………………………………3分
………………………………3分
由 ……………………………………4分
……………………………………4分
 ……………………………………5分
……………………………………5分
又AB∩AV=A
∴AB⊥平面VAD…………………………………………………………………………6分
(Ⅱ)由(Ⅰ)得 是面VAD的法向量………………………………7分
是面VAD的法向量………………………………7分
设 是面VDB的法向量,则
是面VDB的法向量,则
 ……9分
……9分
∴ ,……………………………………11分
,……………………………………11分
又由题意知,面VAD与面VDB所成的二面角,所以其大小为 …………12分
…………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com