练习册

  • 练习册
  • 试题
    20． 【查看更多】

     

    题目列表(包括答案和解析)

    （本题满分13分）

    已知数列满足，

    （1）计算的值；

    （2）由（1）的结果猜想的通项公式，并证明你的结论。

    查看答案和解析>>

    （本题满分13分）

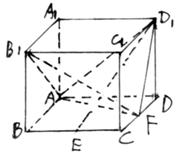
    如图在棱长为2的正方体中，点F为棱CD中点，点E在棱BC上

    （1）确定点E位置使面；

    （2）当面时，求二面角的平面角的余弦值；

     

     

     

     

     

     

     

     

     

    查看答案和解析>>

    （本题满分13分）

    一个口袋里有4个不同的红球，6个不同的白球（球的大小均一样）

    （1）从中任取3个球，恰好为同色球的不同取法有多少种？

    （2）取得一个红球记为2分，一个白球记为1分。从口袋中取出五个球，使总分不小于7分的不同取法共有多少种？

    查看答案和解析>>

    （本题满分13分）已知定义域为[0,1]的函数同时满足：  ①对于任意的,总有;  ②=1;     ③当时有.

    (1)求的值；w.w.w.k.s.5.u.c.o.m        

    (2)求的最大值；

    (3)当对于任意，总有成立，求实数的取值范围.

    查看答案和解析>>

    （本题满分13分）

    已知椭圆的左、右焦点分别为、，过的直线交椭圆于、两点，过的直线交椭圆于、两点，且，垂足为．

    （1）设点的坐标为，求的最值；

    （2）求四边形的面积的最小值．

    查看答案和解析>>

     

    1-5 DCACC            6-10 ABACA

    11.1或-3   12．12    13． 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。     14．15   15．高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    16．解：因为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    所以  高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    故    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。                                     …………6分

         令高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的单调递增的正值区间是

         高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

         单调递减的正值区间是高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。          

    当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，函数高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的单调递增区间为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，函数高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的单调递增区间为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。  （注：区间为开的不扣分）…………12分

    17．（本题满分12分）

    解：（Ⅰ）记“该学生恰好经过4次测试考上大学”的事件为事件A，则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。……6分

    （Ⅱ）记“该生考上大学”的事件为事件B，其对立事件为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 ∴高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 ……12分

     

    18．解：（1）当M为PC的中点时，PC⊥平面MDB．------------------1分

    事实上，连BM，DM，取AD的中点N，连NB，NP．

    因为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，且平面PAD高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。平面ABCD，所以PN⊥平面ABCD．

    在高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。中，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，又高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，又高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。平面MDB，

    而PD=DC=2，所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。平面MDB------------------6分

    （2）易知G在中线BM上，过M作高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。于F，连CF，

    因为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。平面MDB，所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    故高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。是二面角G―BD―C的平面角    ------------------9分

    在高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。中，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，又高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，故二面角G―BD―C的大小为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。----------------12分

    19．21.解：（1）三个函数的最小值依次为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    由高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 

    ∴高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    故方程高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的两根是高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．

    故高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。． 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    ∴  高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．………………6分

    （2）①依题意高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。是方程高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的根，

    故有高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    且△高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．

    由高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。……………9分

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。；得，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．

    由（1）知高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，故高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    ∴  高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    ∴  高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．………………………12分

    20．（1）解法一：设高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,则

          高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。两式相减，得： 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    又 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    可得  高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。……………………………………（5分）

       解法二：设高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,，直线高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。①

       高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

      高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。， 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，又高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。     高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    由条件：高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。……………………………………………………………………（5分）

    （2）由①及高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，可知高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。代入椭圆方程，得

       高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。………………………………………………………………………（10分）

       又高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。  高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。      高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

        高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。…………………………………………………（13分）

    21.解: (Ⅰ)依题意有高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,于是高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.

    所以数列高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。是等差数列.                      ………………….2分

    (Ⅱ)由题意得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 , (高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。)         ①

    所以又有高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.                        ②    ………4分

    由②高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。①得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,

    可知高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。都是等差数列.那么得

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.    (高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。       

    故高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。                            …………8分

    (Ⅲ)当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。为奇数时,高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。为偶数时,高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。  

    作高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。轴,垂足为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,要使等腰三角形高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。为直角三角形,必须且只需高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.                 

    当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。为奇数时,有高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 .             ①

    当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时,高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。;当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时,高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。;当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。, ①式无解.

    当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。为偶数时,有高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,同理可求得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.      

    综上所述,上述等腰三角形高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。中存在直角三角形,此时高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的值为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。或高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    或高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.                                     ……………………..14分

     

     

     


    同步练习册答案