
题目列表(包括答案和解析)
据《中国新闻网》10月21日报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改”引起广泛关注.为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查,就是否“取消英语听力”的问题,调查统计的结果如下表:
| 应该取消 | 应该保留 | 无所谓 |
在校学生 | 2100人 | 120人 | y人 |
社会人士 | 600人 | x人 | z人 |
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.05.
(Ⅰ)现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(Ⅱ)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数ξ的分布列和数学期望.
(本小题满分12分)某校从参加高一年级期末考试的学生中抽出60名学生,将其某科成绩(是不小于40不大于100的整数)分成六段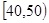 ,
,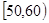 …
…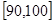 后画出如下频率分布直方图,根据图形中所给的信息,回答以下问题:
后画出如下频率分布直方图,根据图形中所给的信息,回答以下问题:
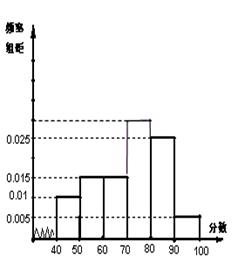
(1)求第四小组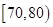 的频率.
的频率.
(2)求样本的众数.
(3) 观察频率分布直方图图形的信息,估计这次考试的及格率(60分及以上为及格)和平均分.
据《中国新闻网》10月21日报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改”引起广泛关注.为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查,就是否“取消英语听力”的问题,调查统计的结果如下表:
| 应该取消 | 应该保留 | 无所谓 | ||
| 在校学生 | 2100人 | 120人 | y人 | ||
| 社会人士 | 600人 | x人 | z人 |
(本小题满分12分)某校从参加高一年级期末考试的学生中抽出60名学生,将其某科成绩(是不小于40不大于100的整数)分成六段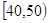 ,
,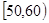 …
…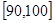 后画出如下频率分布直方图,根据图形中所给的信息,回答以下问题:
后画出如下频率分布直方图,根据图形中所给的信息,回答以下问题: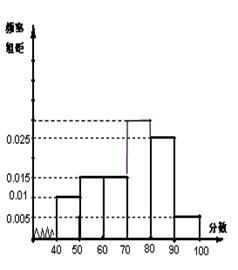
(1)求第四小组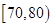 的频率.
的频率.
(2)求样本的众数.
(3) 观察频率分布直方图图形的信息,估计这次考试的及格率(60分及以上为及格)和平均分.

| 应该取消 | 应该保留 | 无所谓 | ||
| 在校学生 | 2100人 | 120人 | y人 | ||
| 社会人士 | 600人 | x人 | z人 |
一、DDBCD CABCA
二、11.1;
12. ; 13.
; 13. 14.
14. ; 15.
; 15. ;
;
16.
三.解答题(本大题共6小题,共76分)
17.解:(1)法一:由题可得 ;
;
法二:由题 ,
,
故 ,从而
,从而 ;
;
法三:由题 ,解得
,解得 ,
,
故 ,从而
,从而 。
。
(2) ,令
,令 ,
,
则 ,
,
 在
在 单调递减,
单调递减,
故
 ,
,
从而 的值域为
的值域为 。
。
18.解:(1) 的可能取值为0,1,2,3,4,
的可能取值为0,1,2,3,4, ,
,

 ,
,
 ,
, ,
,
 。
。
因此随机变量 的分布列为下表所示;
的分布列为下表所示;

0
1
2
3
4






(2)由⑴得: ,
,

19.法一:(1)连接 ,设
,设 ,则
,则 。
。
因为 ,所以
,所以 ,故
,故 ,从而
,从而 ,
,
故 。
。
又因为 ,
,
所以 ,当且仅当
,当且仅当 取等号。
取等号。
此时 为
为 边的中点,
边的中点, 为
为 边的中点。
边的中点。
故当 为
为 边的中点时,
边的中点时, 的长度最小,其值为
的长度最小,其值为
(2)连接 ,因为此时
,因为此时 分别为
分别为 的中点,
的中点,
故 ,所以
,所以 均为直角三角形,
均为直角三角形,
从而 ,所以
,所以 即为直线
即为直线 与平面
与平面 所成的角。
所成的角。
因为 ,所以
,所以 即为所求;
即为所求;
(3)因 ,又
,又 ,所以
,所以 。
。
又 ,故三棱锥
,故三棱锥 的表面积为
的表面积为
 。
。
因为三棱锥 的体积
的体积 ,
,
所以 。
。
法二:(1)因 ,故
,故 。
。
设 ,则
,则 。
。
所以 ,
,
当且仅当 取等号。此时
取等号。此时 为
为 边的中点。
边的中点。
故当 为
为 的中点时,
的中点时, 的长度最小,其值为
的长度最小,其值为 ;
;
(2)因 ,又
,又 ,所以
,所以 。
。
记 点到平面
点到平面 的距离为
的距离为 ,
,
因 ,故
,故 ,解得
,解得 。
。
 因
因 ,故
,故 ;
;
(3)同“法一”。
法三:(1)如图,以 为原点建立空间直角坐标系,设
为原点建立空间直角坐标系,设 ,则
,则 ,
,
所以 ,当且仅当
,当且仅当 取等号。
取等号。
此时 为
为 边的中点,
边的中点, 为
为 边的中点。
边的中点。
故当 为
为 边的中点时,
边的中点时, 的长度最小,其值为
的长度最小,其值为 ;
;
(2)设 为面
为面 的法向量,因
的法向量,因 ,
,
故 。取
。取 ,得
,得 。
。
又因 ,故
,故 。
。
因此 ,从而
,从而 ,
,
所以 ;
;
(3)由题意可设 为三棱锥
为三棱锥 的内切球球心,
的内切球球心,
则 ,可得
,可得 。
。
与(2)同法可得平面 的一个法向量
的一个法向量 ,
,
又 ,故
,故 ,
,
解得 。显然
。显然 ,故
,故 。
。
20.解:(1)当 时,
时, 。令
。令 得
得 ,
,
故当 时
时 ,
, 单调递增;
单调递增;
当 时
时 ,
, 单调递减。
单调递减。
所以函数 的单调递增区间为
的单调递增区间为 ,
,
单调递减区间为 ;
;
(2)法一:因 ,故
,故 。
。
令 ,
,
要使 对满足
对满足 的一切
的一切 成立,则
成立,则 ,
,
解得 ;
;
法二: ,故
,故 。
。
由 可解得
可解得 。
。
因为 在
在 单调递减,因此
单调递减,因此 在
在 单调递增,故
单调递增,故 。设
。设 ,
,
则 ,因为
,因为 ,
,
所以 ,从而
,从而 在
在 单调递减,
单调递减,
故 。因此
。因此 ,即
,即 。
。
(3)因为 ,所以
,所以
即 对一切
对一切 恒成立。
恒成立。
 ,令
,令 ,
,
则 。因为
。因为 ,所以
,所以 ,
,
故 在
在 单调递增,有
单调递增,有 。
。
因此 ,从而
,从而 。
。
所以 。
。
21.解:(1)设 ,则由题
,则由题 ,
,
由 得
得 ,故
,故 。
。
又根据 可得
可得 ,
,
即 ,代入可得
,代入可得 ,
,
解得 (舍负)。故
(舍负)。故 的方程为
的方程为 ;
;
(2)法一:设 ,代入
,代入 得
得 ,
,
故 ,
,
从而


因此 。
。
法二:显然点 是抛物线
是抛物线 的焦点,点
的焦点,点 是其准线
是其准线 上一点。
上一点。
设 为
为 的中点,过
的中点,过 分别作
分别作 的垂线,垂足分别为
的垂线,垂足分别为 ,
,
则 。
。
因此以 为直径的圆与准线
为直径的圆与准线 相切(于点
相切(于点 )。
)。
若 与
与 重合,则
重合,则 。否则点
。否则点 在
在 外,因此
外,因此 。
。
综上知 。
。
22.证明:(1)因 ,故
,故 。
。
显然 ,因此数列
,因此数列 是以
是以 为首项,以2为公比的等比数列;
为首项,以2为公比的等比数列;
(2)由⑴知 ,解得
,解得 ;
;
(3)因为

所以 。
。
又
 (当且仅当
(当且仅当 时取等号),
时取等号),
故 。
。
综上可得 。(亦可用数学归纳法)
。(亦可用数学归纳法)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com