
题目列表(包括答案和解析)
(2009广东卷理)(几何证明选讲选做题)如图4,点![]() 是圆
是圆![]() 上的点, 且
上的点, 且![]() , 则圆
, 则圆![]() 的面积等于 .
的面积等于 .

(2009广东卷理)已知离散型随机变量![]() 的分布列如右表.若
的分布列如右表.若![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
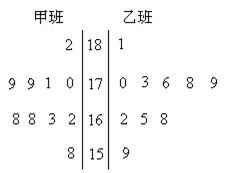
(2009广东)随机抽取某中学甲乙两班各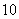 名同学,测量他们的身高(单位:
名同学,测量他们的身高(单位: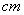 ),获得身高数据的茎叶图如图.
),获得身高数据的茎叶图如图.
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差
(3)现从乙班这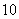 名同学中随机抽取两名身高不低于
名同学中随机抽取两名身高不低于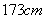 的同学,求身高为
的同学,求身高为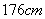 的同学被抽中的概率.
的同学被抽中的概率.
(2009广东卷理)(本小题满分14分)
已知二次函数![]() 的导函数的图像与直线
的导函数的图像与直线![]() 平行,且
平行,且![]() 在
在![]() 处取得极小值
处取得极小值![]() .设
.设![]() .
.
(1)若曲线![]() 上的点
上的点![]() 到点
到点![]() 的距离的最小值为
的距离的最小值为![]() ,求
,求![]() 的值;
的值;
(2)![]() 如何取值时,函数
如何取值时,函数![]() 存在零点,并求出零点.
存在零点,并求出零点.
(2009广东卷理)巳知椭圆![]() 的中心在坐标原点,长轴在
的中心在坐标原点,长轴在![]() 轴上,离心率为
轴上,离心率为![]() ,且
,且![]() 上一点到
上一点到![]() 的两个焦点的距离之和为12,则椭圆
的两个焦点的距离之和为12,则椭圆![]() 的方程为 .
的方程为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com