（2009?四川）如图所示，空气中有一横截面为半圆环的均匀透明柱体，其内圆半径为r，外圆半径为R，R=

2

r．现有一束单色光垂直于水平端面A射入透明柱体，只经过两次全反射就垂直于水平端面B射出．设透明柱体的折射率为n，光在透明柱体内传播的时间为t，若真空中的光速为c，则（　　）

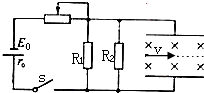（2010?四川）如图所示，电源电动势E₀=15V内阻r₀=1Ω，电阻R₁=30Ω，R₂=60Ω．间距d=0.2m的两平行金属板水平放置，板间分布有垂直于纸面向里、磁感应强度B=1T的匀强磁场．闭合开关S，板间电场视为匀强电场，将一带正电的小球以初速度υ=0.1m/s沿两板间中线水平射入板间．设滑动变阻器接入电路的阻值为R_x，忽略空气对小球的作用，取g=10m/s²．
（1）当R_x=29Ω时，电阻R₂消耗的电功率是多大？
（2）若小球进入板间做匀速度圆周运动并与板相碰，碰时速度与初速度的夹角为60°，则R_x是多少？

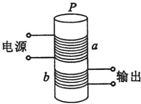（2012?四川）如图所示，在铁芯P上绕着两个线圈a和b，则（　　）

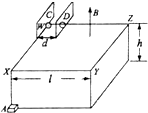（2011?四川）如图所示：正方形绝缘光滑水平台面WXYZ边长l=1.8m，距地面h=0.8m．平行板电容器的极板CD间距d=0.1m且垂直放置于台面，C板位于边界WX上，D板与边界WZ相交处有一小孔．电容器外的台面区域内有磁感应强度B=1T、方向竖直向上的匀强磁场．电荷量q=5×10^-13C的微粒静止于W处，在CD间加上恒定电压U=2.5V，板间微粒经电场加速后由D板所开小孔进入磁场（微粒始终不与极板接触），然后由XY边界离开台面．在微粒离开台面瞬时，静止于X正下方水平地面上A点的滑块获得一水平速度，在微粒落地时恰好与之相遇．假定微粒在真空中运动、极板间电场视为匀强电场，滑块视为质点，滑块与地面间的动摩擦因数μ=0.2，取g=10m/s²
（1）求微粒在极板间所受电场力的大小并说明两板地极性；
（2）求由XY边界离开台面的微粒的质量范围；
（3）若微粒质量m_o=1×10^-13kg，求滑块开始运动时所获得的速度．