
题目列表(包括答案和解析)
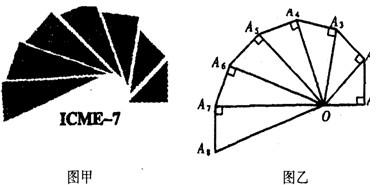
| A、2008 | ||
| B、50 | ||
C、2
| ||
D、
|
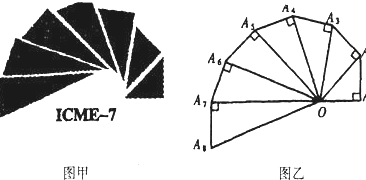
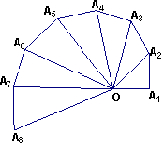 如图是第七届国际数学教育大会(ICME-7)的会徽,它是由一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1,它可以形成近似的等角螺线.记an=|OAn|,n=1,2,3,…,猜想数列{an}的通项公式为
如图是第七届国际数学教育大会(ICME-7)的会徽,它是由一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1,它可以形成近似的等角螺线.记an=|OAn|,n=1,2,3,…,猜想数列{an}的通项公式为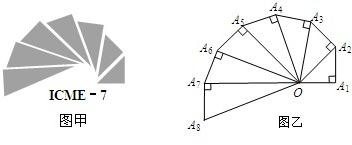 如图甲是第七届国际数学教育大会(简称ICME-7)的会徽图案,会徽的主体图案是由如图乙的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1,如果把图乙中的直角三角形继续作下去,记OA1,OA2,…OAn,…的长度构成数列{an},则此数列的通项公式为an=
如图甲是第七届国际数学教育大会(简称ICME-7)的会徽图案,会徽的主体图案是由如图乙的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1,如果把图乙中的直角三角形继续作下去,记OA1,OA2,…OAn,…的长度构成数列{an},则此数列的通项公式为an=| n |
| n |

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com