甲、乙两名战士在相同条件下各射靶10次，每次命中环数如下：

   甲：8  6  7  8  6  5  9  10  4  7

   乙：6  7  7  8  6  7  8  7   9  5

（1）     分别计算以上两组数据的平均数；

（2）     分别求出两组数据的方差；

根据数据计算结果，估计一下谁的射击水平较稳定

2010年11月广州成功举办了第十六届亚运会。在华南理工大学学生会举行的亚运知识有奖问答比赛中，甲、乙、丙同时回答一道有关亚运知识的问题，已知甲回答对这道题目的概率是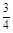，甲、丙两人都回答错的概率是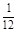，乙、丙两人都回答对的概率是．

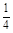（1）求乙、丙两人各自回答对这道题目的概率．

（2）（理）求回答对这道题目的人数的随机变量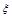的分布列和期望．

【解析】本试题主要考查了独立事件概率的乘法计算公式的运用。以及对立事件的概率的运用。