
题目列表(包括答案和解析)
(12分)重力势能是由地球和地面上物体的相对位置决定的,重力势能的变化只能是由重力做功引起的;弹性势能是由发生弹性形变的物体各部分的相对位置决定的,弹性势能的变化只能是由弹力做功引起的,沿着这个思路,请你探究下面的问题。在光滑水平面上有两个小球,假设它们之间存在着相互排斥的力,并且这种力也由两个小球的相对位置决定,因而也存在一种势能,不妨叫做x势能。现使A球固定不动,B球在获得某一速度后向着A球运动。这一过程中,你猜想存在于它们之间的x势能将如何变化?你能说出它们之间相互作用力的功与x势能变化之间的关系吗?
在“探究弹性势能的表达式”的活动中为计算弹簧弹力所做功,把拉伸弹簧的过程分为很多小段,拉力在每小段可以认为是恒力,用各小段做功的代数和代表弹力在整个过程所做的功,物理学中把这种研究方法叫做“微元法”。下面实例中应用到这一思想方法的是
A.根据加速度定义 ,当 ,当 非常小, 非常小, 就可以表示物体在t时刻的瞬时加速度 就可以表示物体在t时刻的瞬时加速度 |
| B.在探究加速度、力和质量三者之间关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系 |
| C.在推导匀变速运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加 |
| D.在不需要考虑物体本身的大小和形状时,用点来代替物体,即质点 |
在“探究弹性势能的表达式”的活动中为计算弹簧弹力所做功,把拉伸弹簧的过程分为很多小段,拉力在每小段可以认为是恒力,用各小段做功的代数和代表弹力在整个过程所做的功,物理学中把这种研究方法叫做“微元法”。下面实例中应用到这一思想方法的是
A.根据加速度定义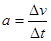 ,当
,当 非常小,
非常小,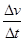 就可以表示物体在t时刻的瞬时加速度
就可以表示物体在t时刻的瞬时加速度
B.在探究加速度、力和质量三者之间关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系
C.在推导匀变速运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加
D.在不需要考虑物体本身的大小和形状时,用点来代替物体,即质点
A.根据加速度定义 ,当 ,当 非常小, 非常小, 就可以表示物体在t时刻的瞬时加速度 就可以表示物体在t时刻的瞬时加速度 |
| B.在探究加速度、力和质量三者之间关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系 |
| C.在推导匀变速运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加 |
| D.在不需要考虑物体本身的大小和形状时,用点来代替物体,即质点 |
在“探究弹性势能的表达式”的活动中为计算弹簧弹力所做功,把拉伸弹簧的过程分为很多小段,拉力在每小段可以认为是恒力,用各小段做功的代数和代表弹力在整个过程所做的功,物理学中把这种研究方法叫做“微元法”。下面实例中应用到这一思想方法的是
A.根据加速度定义![]() ,当
,当![]() 非常小,
非常小,![]() 就可以表示物体在t时刻的瞬时加速度
就可以表示物体在t时刻的瞬时加速度
B.在探究加速度、力和质量三者之间关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系
C.在推导匀变速运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加
D.在不需要考虑物体本身的大小和形状时,用点来代替物体,即质点
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com