
题目列表(包括答案和解析)
⑴证明:函数 f ( x ) =![]() 在区间( 0,
在区间( 0,![]() )上是单调递减的函数(已知在区间( 0,
)上是单调递减的函数(已知在区间( 0,![]() )上有sin x < x < tan x);
)上有sin x < x < tan x);
⑵证明:当0 < x <![]() 时,sin x >
时,sin x >![]() x;
x;
⑶证明:当0 < x <![]() 时,sin x <
时,sin x <![]() ?
?![]() 。
。
(Ⅰ)设函数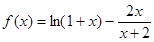 ,证明:当
,证明:当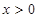 时,
时,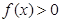 ;
;
(Ⅱ)从编号1到100的100张卡片中每次随机抽取一张,然后放回,用这种方式连续抽取20次,设抽得的20个号码互不相同的概率为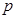 。证明:
。证明: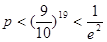 。
。
注:可用(Ⅰ)的结论。
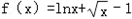 ,证明:
,证明: ( x-1);
( x-1);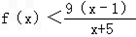 。
。设函数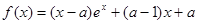 ,
,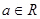 。
。
(1)当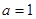 时,求
时,求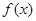 的单调区间;
的单调区间;
(2)(i)设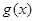 是
是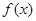 的导函数,证明:当
的导函数,证明:当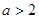 时,在
时,在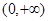 上恰有一个
上恰有一个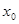 使得
使得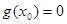 ;
;
(ii)求实数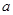 的取值范围,使得对任意的
的取值范围,使得对任意的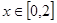 ,恒有
,恒有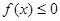 成立。
成立。
注: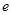 为自然对数的底数。
为自然对数的底数。
设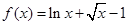 ,证明:
,证明:
(Ⅰ)当x﹥1时,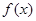 ﹤
﹤ 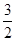 (
( 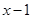 );
);
(Ⅱ)当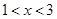 时,
时,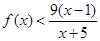 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com