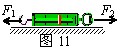
如图11所示，一个准确的弹簧秤，置于粗糙的水平地面上，用F₁＝5N的水平力拉秤钩，用F₂＝6N的水平力拉另一端的圆环，弹簧秤处于静止状态。这时弹簧秤受到的静摩擦力大小是_______N，方向___________。弹簧秤的示数为_______N。

在力的分解中，分力一定比合力小吗？“一指断铁丝”的实验将帮你回答这个问题．

取两根长约15 cm的硬木条，中间用铰链连接，做成“人”字形支架．再取两块硬木，加工成L形，如图2－6－22所示．弯处钉上铁皮，下面装有小铁钩，另备一根细铁丝．

图2－6－22

实验时，把铁丝分别拴在两个小木块的铁钩上，使放在L形木块铁皮上的“人”字形支架张角在160°以上．用一个手指在“人”字形木条的铰链处用力往下按，铁丝即被拉断．想想看并试一试，缩短细铁丝长度，使“人”字形支架张角约为90°时，用相同的力往下按，铁丝能被拉断吗？为什么？

【解析】：当用力向下压“人”字形木条时，把压力F沿支架方向分解

如图则有

F₁＝F₂＝/sin(90°－)

＝/cos故θ越大，cos越小，F₁或F₂越大，铁丝越容易被拉断，当θ减小时，cos增大，则分力F₁、F₂减小，铁丝不易被拉断．

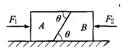
如图所示，两个光滑的梯形木块A和B紧挨着并排放在光滑水平面上，已知θ＝60°，m_A＝2kg，m_B＝1kg，现同时施水平力F₁＝5N作用于A，F₂＝2N作用于B，作用的方向相反。两木块在运动中无相对滑动，则B对A的作用力大小为_______N。

如图所示，物体a、b和c叠放在水平桌面上，水平为F_b＝5N、F_c＝10N分别作用于物体b、c上，a、b和c仍保持静止。以f₁、f₂、f₃分别表示a

与b、b与c、c与桌面间的静摩擦力的大小，则（     ）

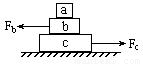
A  f₁＝5N，f₂＝0，f₃＝5N     B  f₁＝5N，f₂＝5N，f₃＝0

C  f₁＝0，f₂＝5N，f₃＝5N     D  f₁＝0，f₂＝10N，f₃＝5N

将一大小F＝10N的力分解成F₁和F₂，则F₁和F₂可能存在的情况是

1. A.
   F₁＝5N，F₂＝25N
2. B.
   F₁＝1N，F₂＝13N
3. C.
   F₁＝500N，F₂＝505N
4. D.
   F₁＝10N，F₂＝36N