练习册

  • 练习册
  • 试题
    29．自然界的大麻为雌雄异株植物. 右图为其性染色体简图.X和Y染色体有一部分是同 源的.该部分基因互为等位,另一部分 是非同源的片段.该部分基因 不互为等位.在研究中发现.大麻种群中的雌雄个体 均有抗病和不抗病个体存在.已知该抗病形状受显性 基因B控制. (1)大麻的性别决定方式为 . (2)由题目信息可知.控制大麻是否具有抗性的基因不可能位于图中的 片段. (3)雄株在减数分裂过程中.不可能通过互换发生基因重组的是图中的 片段. (4)现有抗病的雌.雄大麻若干株.只做一代杂交试验.推测杂交子一代可能出现的性状.并以此为依据.对控制该性状的基因位于除第(2)问外的哪个片段做出相应的推断.如果子一代的行装表现为雌株和雄株中多数为抗病.少数不抗病.那么控制该性状的基因位于图中的 片段,如果子一代的性状表现为 .那么控制该性状的基因位于图中的 片段. (5)若通过实验已确定控制该性状的基因位于Ⅱ-2片段.想通过杂交试验培育一批在生殖生长之前就能识别雌雄的植株.则选择的亲本中雄株表现型为 .其基因型为 .子代的性状表现型为 . 【查看更多】

     

    题目列表(包括答案和解析)

    计算（ 每题 6分，共18分） 

       （1）2log525 + 3log264     （2）     （3） =

     

     

    查看答案和解析>>

    已知抛物线y2＝8x的准线与双曲线－＝1(a>0，b>0)相交于A，B两点，双曲线的一条渐近线方程是y＝2x，点F是抛物线的焦点，且△FAB是直角三角形，则双曲线的标准方程是(　　)

    (A)－＝1         (B)x2－＝1

    (C)－＝1         (D)－y2＝1

    二、填空题(每小题6分，共18分)

    查看答案和解析>>

    （本题共3小题，每小题6分，满分18分）

    已知函数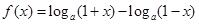

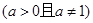
    （1）讨论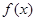的奇偶性与单调性；

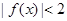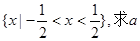    （2）若不等式的解集为的值；

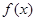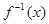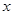    （3）设的反函数为，若关于的不等式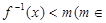R）有解，求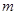的取值范围.

     

    查看答案和解析>>

    [选做题]本题包括A、B、C、D共4小题，请从这4小题中选做2小题，每小题10分，共20分．
    A．如图，AD是∠BAD的角平分线，⊙O过点A且与BC边相切于点D，与AB，AC分别交于E、F两点．求证：EF∥BC．
    B．已知M=
    .
    1-2
    3-7
    .
    ，求M-1．
    C．已知直线l的极坐标方程为θ=
    π
    4
    （ρ∈R），它与曲线C
    x=1+2cosα
    y=2+2sinα
    （α为参数）相较于A、B两点，求AB的长．
    D．设函数f（x）=|x-2|+|x+2|，若不等式|a+b|-|4a-b|≤|a|，f（x）对任意a，b∈R，且a≠0恒成立，求实数x的取值范围．

    查看答案和解析>>

    [选做题]在下面A，B，C，D四个小题中只能选做两题，每小题10分，共20分．
    A．选修4-1：几何证明选讲
    如图，⊙O是等腰三角形ABC的外接圆，AB=AC，延长BC到点D，使CD=AC，连接AD交⊙O于点E，连接BE与AC交于点F，判断BE是否平分∠ABC，并说明理由．
    B．选修4-2：短阵与变换
    已知矩阵M=
    1
    2
    		0
    02
    ，矩阵M对应的变换把曲线y=sinx变为曲线C，求C的方程．
    C．选修4-4：坐标系与参数方程
    已知曲线C的极坐标方程是ρ=4sin(θ+
    π
    4
    )    ，求曲线C的普通方程．
    D．选修4-5：不等式选讲
    已知x，y，z∈R，且x+y+z=3，求x2+y2+z2的最小值．

    查看答案和解析>>


    同步练习册答案