
题目列表(包括答案和解析)
(本小题13分)
有一批单放机原价为每台80元,两个商场均有销售,为了吸引顾客,两商场纷纷推出优惠政策。甲商场的优惠办法是:买一台减4元,买两台每台减8元,买三台每台减12元,......,依此类推,直到减到半价为止;乙商场的优惠办法是:一律7折。某单位欲为每位员工买一台单放机,问选择哪个商场购买比较划算?
(本小题13分)某饮料生产企业为了占有更多的市场份额,拟在2010年度进行
一系列促销活动,经过市场调查和测算,饮料的年销售量x万件与年促销费t万元间满足
 。已知2010年生产饮料的设备折旧,维修等固定费用为3 万元,每生产1万件
。已知2010年生产饮料的设备折旧,维修等固定费用为3 万元,每生产1万件
饮料需再投入32万元的生产费用,若将每件饮料的售价定为:其生产成本的150%与平均
每件促销费的一半之和,则该年生产的饮料正好能销售完。
(1)将2010年的利润y(万元)表示为促销费t(万元)的函数;
(2)该企业2010年的促销费投入多少万元时,企业的年利润最大?
(注:利润=销售收入—生产成本—促销费,生产成本=固定费用+生产费用)
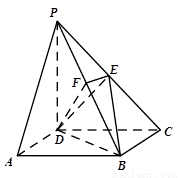
(本小题13分)如图,在四棱锥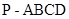 中,
中,
底面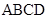 是矩形,侧棱PD⊥底面
是矩形,侧棱PD⊥底面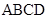 ,
,
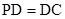 ,
,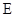 是
是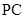 的中点,作
的中点,作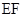 ⊥
⊥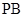 交
交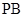 于点
于点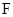 .
.
(1)证明: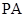 ∥平面
∥平面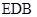 ;
;
(2)证明: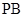 ⊥平面
⊥平面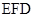 .
.
(本小题13分)已知数列{an}的前n项和Sn = 2an – 3×2n + 4 (n∈N*)
(1)求数列{an}的通项公式an;(2)设Tn为数列{Sn – 4}的前n项和,试比较Tn与14的大小.
(本小题13分)已知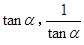 是关于
是关于 的方程
的方程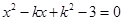 的两个实根,且
的两个实根,且 ,求
,求 的值
的值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com