
题目列表(包括答案和解析)
下列计算中错误的是
A.0.25°=![]()
B.![]()
C.32.15°=![]()
D.![]()
观察下列等式:
(1)32-12=4×2;
(2)42-22=4×3;
(3)52-32=4×4;
(4)( )2-( )2=( )×( );
……
则第4个等式为________.第n个等式为________.(n是正整数)
如图,若AB是⊙0的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD=
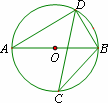
A.116°
B.32°
C.58°
D.64°
孙海洋是个爱动脑筋的八年级学生,他特别喜欢数学,一有空就看数学课外书,并琢磨书上的问题.有一次,他从一本书中看到了下面一个有趣的问题:
仔细观察下面4个等式:
32=2+22+3
42=3+32+4
52=4+42+5
62=5+52+6
……
请写出第5个等式,由此能发现什么规律?用公式将发现的规律表示出来.
对这个问题,孙海洋感到很新奇,他认真分析题目给出的4个等式,发现有以下一些结构特征:
(1)每个等式的左边都是一个自然数的平方,等式的右边都是3个数的和.
(2)4个等式的左边依次是32、42、52、62,它们的底数3、4、5、6是4个连续的自然数,其大小均比所处等式的序号多2.
(3)每个等式右边的3个加数也有明显的规律.
第1个加数和第3个加数是两个连续的自然数,并且第3个加数等于该等式左边平方数的底数,第2个加数也是一个平方数,底数等于第1个加数.
根据以上规律,孙海洋猜想第5个等式应该是72=6+62+7.
孙海洋进一步归纳了这5个等式的规律,用公式表示为(n+1)2=n+n2+(n+1)…①其中n=2,3,…
如果将①式右边变形、左边不变,那么可得(n+1)2=n2+2n+1…②
等式②多么眼熟啊!它不就是完全平方公式的一个具体应用吗?由此可见,孙海洋同学归纳的规律是正确的.
想一想,当n=0,1时,等式①是否成立?当n为负整数时,等式①是否成立?
如图,AB∥CD,∠B=23°,∠D=32°,则∠E=
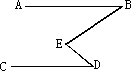
A.23°
B.42°
C.65°
D.55°
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com