(2004江苏，19)制订投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损．某投资人打算投资甲、乙两个项目，根据预测，甲、乙项目可能的最大盈利率分别为100％和50％，可能的最大亏损率分别为30％和10％，投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元，问投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？

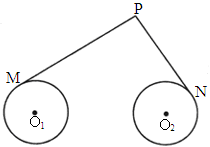
(2005江苏，19)如图所示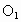，圆和圆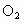的半径都等于1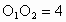，．过动点P分别作圆、圆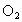的切线PM、PN(M、N为切点)，使得．试建立平面直角坐标系，并求动点P的轨迹方程．

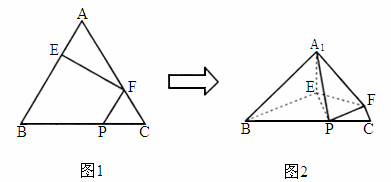
(2006江苏，19)如下图，在正三角形ABC中，E、F、P分别是AB、AC、BC边上的点，满足AE∶EB=CF∶FA=CP∶PB=l∶2(如图1)．将△AEF沿EF折起到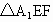的位置，使二面角成直二面角，连结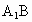、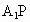(如图2)．

(1)求证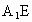：⊥平面BEP；

(2)求直线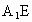与平面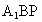所成角的大小；

(3)求二面角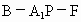的大小(用反三角函数值表示)．

（2012年高考江苏卷19） （本小题满分16分）

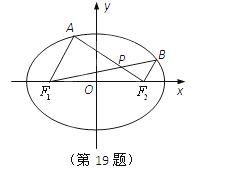如图，在平面直角坐标系xOy中，椭圆的左、右焦点分别为，．已知和都在椭圆上，其中e为椭圆的离心率．

（1）求椭圆的离心率；

（2）设A，B是椭圆上位于x轴上方的两点，且直线

与直线平行，与交于点P．

（i）若，求直线的斜率；

（ii）求证：是定值．

（09年江苏模拟）某高级中学共有学生2000人，各年级男、女生人数如下表：

已知在全校学生中随机抽取1名，抽到高二年级女生的概率是0.19.

（Ⅰ）现用分层抽样的方法在全校抽取48名学生，问应在高三年级抽取多少人？

（Ⅱ）已知求高三年级女生比男生多的概率.