
题目列表(包括答案和解析)
已知关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根
有两个不相等的实数根
(1)求![]() 的取值范围;
的取值范围;
(2)若![]() 为正整数,且该方程的根都是整数,求
为正整数,且该方程的根都是整数,求![]() 的值。
的值。
已知关于 的一元二次方程
的一元二次方程 有两个不相等的实数根.
有两个不相等的实数根.
(1)求 的取值范围;
的取值范围;
(2)若 为正整数,且该方程的根都是整数,求
为正整数,且该方程的根都是整数,求 的值.
的值.
已知关于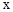 的一元二次方程
的一元二次方程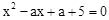 .
.
(1)若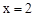 是该方程的一个根,求
是该方程的一个根,求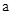 的值;
的值;
(2)无论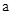 取任何值,该方程的根不可能为
取任何值,该方程的根不可能为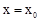 ,写出
,写出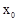 的值,并证明;
的值,并证明;
(3)若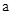 为正整数,且该方程存在正整数解,求所有正整数
为正整数,且该方程存在正整数解,求所有正整数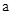 的值.
的值.
已知关于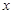 的一元二次方程
的一元二次方程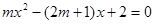 .
.
(1)求证:此方程总有两个实数根;
(2)若此方程的两个实数根都是整数,求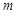 的整数值;
的整数值;
(3)若此方程的两个实数根分别为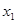 、
、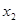 ,求代数式
,求代数式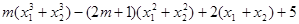 的值.
的值.
已知关于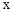 的一元二次方程
的一元二次方程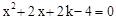 有两个不相等的实数根
有两个不相等的实数根
(1)求 的取值范围;
的取值范围;
(2)若 为正整数,且该方程的根都是整数,求
为正整数,且该方程的根都是整数,求 的值。
的值。
一、选择题:(共8个小题,每小题4分,共32分)
题号
1
2
3
4
5
6
7
8
答案
C
B
C
B
A
D
D
A
二、填空题:(共4个小题,每小题4分,共16分)
9.x≥-3 10.2(x-1)2 11.60° 12.±1
三、解答题:(共5个小题,每小题5分,共25分)
13.解:原式= +1+2-6×
+1+2-6× .
4分
.
4分
=3. 5分
14.解:去分母,得3(x+1)+2x(x-1)=2(x-1)(x+1). 2分
去括号,得3x+3+2x2-2x=2x2-2. 3分
解得x=-5. 4分
经检验x=-5是原方程的解. 5分
∴原方程的解是x=-5.
15.解:x(x2-x)+x2(6-x)+3=x3-x2+6x2-x3+3. 3分
=5x2+3. 4分
∴原式=13. 5分
16.证明:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.BC=CA. 2分
∴∠DBC=∠ECA=180°-60°=120°. 3分

在△DBC与△ECA中,

∴△DBC≌△ECA. 4分
∴DC=AE. 5分
17.解:过点A、D分别作AE⊥BC、DF⊥BF,垂足分别为点E、F. 1分

(第17题图)
在Rt△DCF中,∠DFC=90°.
由CD=4,cos∠C= ,
,
得CF=CD?cos∠C=4× =1.
2分
=1.
2分
在梯形ABCD中,由AD∥BC,AB=CD,
∴∠B=∠C.
同理:BE=1 3分
易证四边形AEFD为矩形.
∴EF=AD=4 4分
∴BC=6
∴梯形ABCD的周长为AD+AB+DC+BC=18 5分
四、解答题:(共2个小题,每小题5分,共10分)
18.解:(1)因为一次函数y=2x-1的图象经过点(k,5),
∴5=2k-1.
∴k=3.
所以反比例函数的解析式为y= . 2分
. 2分
(2)由题意得:
解这个方程组得: 4分
4分
因为点A在等一象限,则x>0,y>0
所以点A的坐标为( ,2). 5分
,2). 5分
19.(1)2400. 2分
(2)如图. 3分

(3)∵200× =50(万人),
=50(万人),
∴18~23岁的网瘾人数约有50万人. 5分
五、解答题:(共2个小题,每小题5分,共10分)
20.解:设日用品类的销售额为x万元,烟酒类的销售额为y万元. 1分
依题意得, 3分
3分
解得 4分
4分
答:日用品的销售额为12万元,烟酒类销售额为60万元. 5分
21.(1)证明:∵AB=AC,∴∠ABC=∠C,

∵∠C=∠D,∴∠ABC=∠D.
又∵∠BAE=∠DAB,
∴△ABE~△ADB. 2分
(2)连接OA.
∵BD为⊙O的直径,∴∠BAD=90°.
Rt△BAD中,tan∠ADB= .
.
∴∠ADB=30°
∵AB= BD,BF=BO=AB.
BD,BF=BO=AB.
∴△ABO是等边三角形.∴∠ABO=∠OAB=60°.
又可得∠BAF=30°.
∴∠OAF=∠OAB+∠BAF=90°.
∴FA是⊙O的切线. 5分
六、解答题:(本题满分5分)
22.(1)(2)各2分,(3)答案不唯一 1分.

七、解答题:(本题满分7分)
23.解:(1)根据题意,得 解得
解得
∴抛物线的解析式为y=-x2-4x+5. 2分
顶点D的坐标为(-2,9). 3分
(2)由抛物线的解析式y=-x2-4x+5.可得C点的坐标为(-5,0).
∵B点的坐标为(0,5),
∴直线CB的解析式为y=x+5.
<?>当OP∥CD,且OP≠CD时,四边形PDCO为梯形.
∵直线CD的解析式为y=3x+15,OP∥CD,
∴直线OP的解析式为y=3x.
根据题意,得 解得
解得
∴点P
 .
.
∵OP= ,CD=
,CD= ,
,
∴OP≠CD.
∴点P
 即为所求.
5分
即为所求.
5分
<ii>当DP∥CO,且DP≠CO时,四边形PDCO为梯形.
根据题意, 解得
解得
∴点P(4,9).
∵OC=5,DP=6,
∴OC≠DP.
∴点P(4,9)即为所求. 7分
综上所述,使四边形PDCO为梯形的点P分别是P1 ,P2(4,9).
,P2(4,9).
八、解答题:(本题满分7分)
24.(1)∵S△POA?S△PBC
= ×50×15×
×50×15× ×50×35=252×15×35,
×50×35=252×15×35,
S△PAB?S△POC= ×50×30×
×50×30× ×50×20=252×30×20,
×50×20=252×30×20,
∴S△POA?S△PBC≠S△PAB?S△POC. 2分
∴P(20,15)不是“好点”. 3分
(2)设P(x,y)其中x,y均为正整数,且0<x<50,0<y<50. 4分
由S△POA?S△PBC=S△PAB?S△POC,
得y(50-y)=x(50-x),
(x-y)(x+y-50)=0
∴x=y或x+y=50. 6分
于是,点P在对角线OB或AC上.
故满足条件的好点共有2×49-1=97个. 7分
九、解答题:(本题满分8分)
解:(1)S四边形AEDF= .
1分
.
1分
(2)过点D作DM⊥AB,垂足为点M,
y= BE?DM=
BE?DM= (3-x)?
(3-x)? (3-x)(0≤x≤3). 3分
(3-x)(0≤x≤3). 3分
(3)<i>如图a:连接AD,过点D分别作AB、AC的垂线,垂足为M,N

图a
∵AB=AC=3,∠BAC=90°,
∴BC= .
.
∵BD=2CD,∴BD= ,CD=
,CD= .
.
易得,DN=1,DM=2,
易证∠1=∠2,
∠DME=∠DNF=90°
∴△DME∽△DNF.
∴ .
.
∴ME=2(x-1).
∴AE=2(x-1)+1=2x-1.
∴y=S△ADE+S△ADF= (2x-1)?2+
(2x-1)?2+ (3-x)?1=
(3-x)?1= x+
x+ (1<x≤2).
6分
(1<x≤2).
6分
<ii>如图b:过点D作AC的垂线,垂足为N,

图b
∵AB=AC=3,∠BAC=90°,
∴BC= .
.
∵BD=2CD,∴BD= ,CD=
,CD= .
.
易得,DN=1,y=S△ABC-S△CDF = ?1=
?1= (2<x≤3) 8分
(2<x≤3) 8分
∴y=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com