
过点D作AB的平行线交BC于点F,以D为
原点,DE为x轴,DF为y轴,
DP为z轴,建立如图所示的空间直角坐标系.
则D(0,0,0),P(0,0, ),
),
E( ),B=(
),B=( )
)

设 上平面PAB的一个法向量,
上平面PAB的一个法向量,
则由

这时, ……………………6分
……………………6分
显然, 是平面ABC的一个法向量.
是平面ABC的一个法向量.
∴
∴二面角P―AB―C的大小是 ……………………8分
……………………8分
(3)解:

设 平面PBC的一个法向量,
平面PBC的一个法向量,
由
得
令 是平面PBC的一个法向量……………………10分
是平面PBC的一个法向量……………………10分
又
∴点E到平面PBC的距离为 ………………12分
………………12分
19.解:(1)由题设,当价格上涨x%时,销售总金额为:
(2)
即 ……………………3分
……………………3分
当
当x=50时,
即该吨产品每吨的价格上涨50%时,销售总最大.……………………6分
(2)由(1)
如果上涨价格能使销假售总金额增加,
则有 ……………………8分
……………………8分
即x>0时,
∴
注意到m>0
∴ ∴
∴ ∴
∴
∴m的取值范围是(0,1)…………………………12分
20.解(1)由已知,抛物线 ,焦点F的坐标为F(0,1)………………1分
,焦点F的坐标为F(0,1)………………1分
当l与y轴重合时,显然符合条件,此时 ……………………3分
……………………3分
当l不与y轴重合时,要使抛物线的焦点F与原点O到直线l的距离相等,当且仅当直线l通过点( )设l的斜率为k,则直线l的方程为
)设l的斜率为k,则直线l的方程为
由已知可得 即
即 ………5分
………5分
解得 无意义.
无意义.
因此,只有 时,抛物线的焦点F与原点O到直线l的距离相等.……7分
时,抛物线的焦点F与原点O到直线l的距离相等.……7分
(2)由已知可设直线l的方程为 ……………………8分
……………………8分
则AB所在直线为 ……………………9分
……………………9分
代入抛物线方程 ………………①
………………①
∴ 的中点为
的中点为
代入直线l的方程得: ………………10分
………………10分
又∵对于①式有:
解得m>-1,
∴
∴l在y轴上截距的取值范围为(3,+ )……………………12分
)……………………12分
21.解:(1)由
得 ……………………3分
……………………3分
又由已知
∴
∴
∴数列 是以3为首项,以-1为公差的等差数列,且
是以3为首项,以-1为公差的等差数列,且 …………6分
…………6分
(2)∵ ……………………8分
……………………8分
∴ …………①
…………①
 …………②………………10分
…………②………………10分
②―①得

 ……………………12分
……………………12分
22.解:(1) 和[0,2]上有相反的单调性,
和[0,2]上有相反的单调性,
∴ 的一个极值点,故
的一个极值点,故
(2)令
因为 和[4,5]上有相反的单调性,
和[4,5]上有相反的单调性,
∴
 和[4,5]上有相反的符号,
和[4,5]上有相反的符号,
故 ……………………7分
……………………7分
假设在点M 在点M的切线斜率为3b,则
在点M的切线斜率为3b,则
即
∵
∴
故不存在点M 在点M的切线斜率为3b………………9分
在点M的切线斜率为3b………………9分
(3)∵ 的图象过点B(2,0),
的图象过点B(2,0),
∴
设 ,依题意可令
,依题意可令

则 ……………………12分
……………………12分
∴

∵
∴当
故 ……………………14分
……………………14分

 A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线ρsin(θ+
A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线ρsin(θ+ A.(不等式选做题)不等式|
A.(不等式选做题)不等式|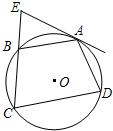 A.如图,四边形ABCD内接于⊙O,弧AB=弧AD,过A点的切线交CB的延长线于E点.
A.如图,四边形ABCD内接于⊙O,弧AB=弧AD,过A点的切线交CB的延长线于E点. A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲 A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲