
题目列表(包括答案和解析)
(本 小题满分14分)
小题满分14分) 已知
已知 是定义在
是定义在 上的函数, 其
上的函数, 其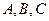 三点, 若点
三点, 若点 的坐标为
的坐标为
 ,且
,且 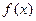 在
在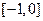 和
和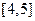 上有相同的单调性, 在
上有相同的单调性, 在 和
和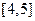 上有相反的单调性.
上有相反的单调性.
(1)求 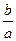 的取值范围;
的取值范围;
(2)在函数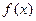 的图象上是否存在一点
的图象上是否存在一点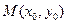 , 使得
, 使得 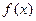 在点
在点 的切线斜率为
的切线斜率为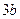 ?求出点
?求出点 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(3)求 的取值范围。
的取值范围。
(本小题满分14分)已知 是定义在[-1,1]上的奇函数,当
是定义在[-1,1]上的奇函数,当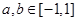 ,且
,且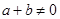 时有
时有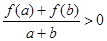 .
.
(1)判断函数 的单调性,并给予证明;
的单调性,并给予证明;
(2)若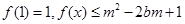 对所有
对所有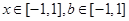 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
(本小题满分14分)
已知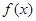 是定义在
是定义在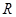 上的偶函数,当
上的偶函数,当 时,
时, .
.
(1)求函数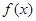 的解析式;
的解析式;
(2)若不等式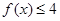 的解集为
的解集为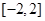 ,求
,求 的值.
的值.
(本小题满分14分)
已知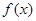 是定义在R上的奇函数,且
是定义在R上的奇函数,且 ,求:
,求:
(1)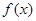 的解析式。
的解析式。
(2)已知 ,求函数
,求函数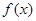 在区间
在区间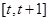 上的最小值。
上的最小值。
(本 小题满分14分)
小题满分14分)
 已知
已知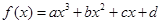 是定义在
是定义在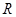 上的函数, 其
上的函数, 其 三点, 若点
三点, 若点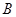 的坐标为
的坐标为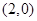
 ,且
,且 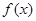 在
在 和
和 上有相同的单调性, 在
上有相同的单调性, 在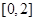 和
和 上有相反的单调性.
上有相反的单调性.
(1)求  的取值范围;
的取值范围;
(2)在函数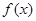 的图象上是否存在一点
的图象上是否存在一点 , 使得
, 使得 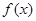 在点
在点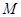 的切线斜率为
的切线斜率为 ?求出点
?求出点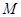 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(3)求 的取值范围。
的取值范围。
一、选择题
|