
题目列表(包括答案和解析)
| ax2+bx+1 |
| cx+d |
| 2 |
| 1 |
| 2 |
| 3 |
| 2x |
 ,且当x>0时,f(x)有最小值
,且当x>0时,f(x)有最小值 ,又f(1)=3.
,又f(1)=3. ,数列{bn}中b1=m(m>0),bn+1=h(bn)(n∈N*).是否存在常数m使bn•bn+1>0对任意n∈N*恒成立.若存在,求m的取值范围,若不存在,说明理由.
,数列{bn}中b1=m(m>0),bn+1=h(bn)(n∈N*).是否存在常数m使bn•bn+1>0对任意n∈N*恒成立.若存在,求m的取值范围,若不存在,说明理由.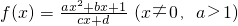 ,且当x>0时,f(x)有最小值
,且当x>0时,f(x)有最小值 ,又f(1)=3.
,又f(1)=3.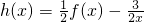 ,数列{bn}中b1=m(m>0),bn+1=h(bn)(n∈N*).是否存在常数m使bn•bn+1>0对任意n∈N*恒成立.若存在,求m的取值范围,若不存在,说明理由.
,数列{bn}中b1=m(m>0),bn+1=h(bn)(n∈N*).是否存在常数m使bn•bn+1>0对任意n∈N*恒成立.若存在,求m的取值范围,若不存在,说明理由.| π | 2 |
| f(x1)-f(x2) | 1+f(x1)f(x2) |
一、选择
1.A 2.B 3.B 4.D 5.(理)C (文)A 6.B 7.A 8.B 9.A
10.B 11.(理)A (文)C 12.B
二、填空
13.(理) (文)25,60,15 14.-672 15.2.5小时 16.(理)①,④(文)(1),
(文)25,60,15 14.-672 15.2.5小时 16.(理)①,④(文)(1), ;(1),
;(1), ;(4),
;(4), 等
等
三、解答题
17.解析:设f(x)的二次项系数为m,其图象上两点为(1-x, )、B(1+x,
)、B(1+x, )因为
)因为 ,
, ,所以
,所以 ,由x的任意性得f(x)的图象关于直线x=1对称,若m>0,则x≥1时,f(x)是增函数,若m<0,则x≥1时,f(x)是减函数.
,由x的任意性得f(x)的图象关于直线x=1对称,若m>0,则x≥1时,f(x)是增函数,若m<0,则x≥1时,f(x)是减函数.
∵  ,
, ,
, ,
, ,
, ,
,
 ,
,
∴ 当 时,
时,




 ,
, .
.
∵  , ∴
, ∴  .
.
当 时,同理可得
时,同理可得 或
或 .
.
综上: 的解集是当
的解集是当 时,为
时,为 ;
;
当 时,为
时,为 ,或
,或 .
.
18.解析:(理)(1)设甲队在第五场比赛后获得冠军为事件M,则第五场比赛甲队获胜,前四场比赛甲队获胜三场
依题意得 .
.
(2)设甲队获得冠军为事件E,则E包含第四、第五、第六、第七场获得冠军四种情况,且它们被彼此互斥.
∴  .
.
(文)①设甲袋中恰有两个白球为事件A

②设甲袋内恰好有4个白球为事件B,则B包含三种情况.
甲袋中取2个白球,且乙袋中取2个白球,②甲袋中取1个白球,1个黑球,且乙袋中取1个白球,1个黑球,③甲、乙两袋中各取2个黑球.
∴ 
 .
.
19.解析:(1)取 中点E,连结ME、
中点E,连结ME、 ,
,
∴ 

 ,MC
,MC EC. ∴
EC. ∴ 
 MC. ∴
MC. ∴  ,M,C,N四点共面.
,M,C,N四点共面.

(2)连结BD,则BD是 在平面ABCD内的射影.
在平面ABCD内的射影.
∵  , ∴ Rt△CDM~Rt△BCD,∠DCM=∠CBD.
, ∴ Rt△CDM~Rt△BCD,∠DCM=∠CBD.
∴ ∠CBD+∠BCM=90°. ∴ MC⊥BD. ∴  .
.
(3)连结 ,由
,由 是正方形,知
是正方形,知 ⊥
⊥ .
.
∵  ⊥MC, ∴
⊥MC, ∴  ⊥平面
⊥平面 .
.
∴ 平面 ⊥平面
⊥平面 .
.
(4)∠ 是
是 与平面
与平面 所成的角且等于45°.
所成的角且等于45°.
20.解析:(1) .
.
∵ x≥1. ∴  ,
,
当x≥1时, 是增函数,其最小值为
是增函数,其最小值为 .
.
∴ a<0(a=0时也符合题意). ∴ a≤0.
(2) ,即27-6a-3=0, ∴ a=4.
,即27-6a-3=0, ∴ a=4.
∴  有极大值点
有极大值点 ,极小值点
,极小值点 .
.
此时f(x)在 ,
, 上时减函数,在
上时减函数,在 ,+
,+ 上是增函数.
上是增函数.
∴ f(x)在 ,
, 上的最小值是
上的最小值是 ,最大值是
,最大值是 ,(因
,(因 ).
).
21.解析:(1)∵ 斜率k存在,不妨设k>0,求出M( ,2).直线MA方程为
,2).直线MA方程为 ,直线MB方程为
,直线MB方程为 .
.
分别与椭圆方程联立,可解出 ,
, .
.
∴  . ∴
. ∴  (定值).
(定值).
(2)设直线AB方程为 ,与
,与 联立,消去y得
联立,消去y得
 .
.
由D>0得-4<m<4,且m≠0,点M到AB的距离为 .
.
设△AMB的面积为S. ∴  .
.
当 时,得
时,得 .
.
22.解析:(1)∵  ,a,
,a, ,
,
∴  ∴
∴  ∴
∴ 
∴  .
.
∴ a=2或a=3(a=3时不合题意,舍去). ∴a=2.
(2) ,
, ,由
,由 可得
可得
 . ∴
. ∴  .
.
∴ b=5
(3)由(2)知 ,
, , ∴
, ∴  .
.
∴  . ∴
. ∴  ,
, .
.
∵  ,
, .
.
当n≥3时,



 .
.
∴  . 综上得
. 综上得 
 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com