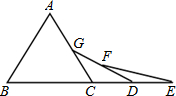18、如图，已知△ABC是等边三角形，点B、C、D、E在同一直线上，且CG=CD，DF=DE，则∠E=

15

度．

查看答案和解析>>

如图，已知抛物线经过坐标原点O和x轴上另一点E，顶点M的坐标为（2，4）；矩形ABCD的顶点A与点O重合，AD、AB分别在x轴、y轴上，且AD=2，AB=3．
（1）求该抛物线所对应的函数关系式；
（2）将矩形ABCD以每秒1个单位长度的速度从如图所示的位置沿x轴的正方向匀速平行移动，同时一动点P也以相同的速度从点A出发向B匀速移动，设它们运动的时间为t秒（0≤t≤3），直线AB与该抛物线的交点为N（如图2所示）．
①当t=

5

2

时，判断点P是否在直线ME上，并说明理由；
②设以P、N、C、D为顶点的多边形面积为S，试问S是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．

查看答案和解析>>

如图，已知△ABC、△DCE、△FEG是三个全等的等腰三角形，底边BC、CE、EG在同一直线上，且AB=

3

，BC=1，连接BF，分别交AC、DC、DE于点P、Q、R．
（1）求证：△BFG∽△FEG，并求出BF的长；
（2）观察图形，请你提出一个与点P相关的问题，并进行解答．（根据提出问题的层次和解答过程评分）

查看答案和解析>>

如图，已知点A、B、C、D、E在同一直线上，且AC=BD，E是线段BC的中点．

（1）点E是线段AD的中点吗？说明理由；
（2）当AD=10，AB=3时，求线段BE的长度．

查看答案和解析>>

如图，已知△ABC和△DEF是两个边长都为1cm的等边三角形，且B、D、C、E都在同一直线上，连接AD及CF．
（1）求证：四边形ADFC是平行四边形；
（2）若BD=0.3cm，△ABC沿着BE的方向以每秒1cm的速度运动，设△ABC运动时间为t秒，
①当t为何值时，?ADFC是菱形？请说明你的理由；
②?ADFC有可能是矩形吗？若可能，求出t的值及此矩形的面积；若不可能，请说明理由．

查看答案和解析>>

选择与填空每题3分

1．D

2．D  点拨：图中的邻补角分别是：∠AOC与∠BOC，∠AOC与∠AOD，∠COE与∠DOE，∠BOE与∠AOE，∠BOD与∠BOC，∠AOD与∠BOD，共6对，故选D．

3．B   4．B   5．D   6．D

7．B

8．A

9．C

10．A

11．B点拨：∠FCD=∠F=∠A=∠1=∠ABG=45°．

故选D．

12．D

13．略 14．略 15．略

16．-4ab

17．红球

 18．145º

19．略 每题4分

20．（3分）-3x+y²               3.25 （3分）  

(2)90 （3分）   41（3分）

21（7分）答图，由邻补角的定义知∠BOC=100°．

    ∵OD，OE分别是∠AOB，∠BOC的平分线，

    ∴∠DOB=∠AOB=40°，∠BOE=∠BOC=50°．

∴∠DOE=∠DOB+∠BOE=40°+50°=90°．

22．（7分）解：CD⊥AB，FE⊥AB，∴CD∥EF，

∴∠2=∠FCD．

∵∠1=∠2，∴∠1=∠FCD．

∴DG∥BC．∴∠BCA=∠3=80°．

23.（7分）  列方程解得边长为5cm

24.（7分）有两个角，有一种不平行。作出一种给3分。

25．（6分）解：AB∥CD．

    理由：如答图，过点F作FH∥AB，则∠AEF+∠EFH=180°．

    ∵∠AEF=150°，∴∠EFH=30°．

    又∵EF⊥GF，∴∠HFG=90°-30°=60°．

    又∵∠DGF=60°，

    ∴∠HFG=∠DGF．

∴HF∥CD，从而可得AB∥CD．