练习册

  • 练习册
  • 试题
    [例2]已知向量..则( ) 【查看更多】

     

    题目列表(包括答案和解析)

    已知向量a=（x-1,2），b=（2,1），则a⊥b的充要条件是

    A.x=-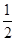  B.x-1   C.x=5    D.x=0

    【解析】有向量垂直的充要条件得2（x-1)+2=0,所以x=0.D正确.

     

    查看答案和解析>>

    已知向量夹角为 ，且；则

    【解析】因为，所以，即，所以，整理得，解得或（舍去）.

     

    查看答案和解析>>

    如图，已知四棱锥的底面ABCD为正方形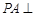，平面ABCD，E、F分别是BC，PC的中点，，．

    （1）求证：平面；

    （2）求二面角的大小．

    【解析】第一问利用线面垂直的判定定理和建立空间直角坐标系得到法向量来表示二面角的。

    第二问中，以A为原点，如图所示建立直角坐标系

    ，，

    设平面FAE法向量为，则

    ，，

     

    查看答案和解析>>

    如图，在三棱柱中，侧面，为棱上异于的一点，，已知，求：

    （Ⅰ）异面直线与的距离；

    （Ⅱ）二面角的平面角的正切值.

    【解析】第一问中，利用建立空间直角坐标系

    解：（I）以B为原点，、分别为Y,Z轴建立空间直角坐标系.由于，

    在三棱柱中有

    ,

    设

    又侧面，故. 因此是异面直线的公垂线，则，故异面直线的距离为1.

    （II）由已知有故二面角的平面角的大小为向量与的夹角.

     

    查看答案和解析>>

    已知正方体ABCD－A1B1C1D1，

      O是底面ABCD对角线的交点.

    （1）求证：A1C⊥平面AB1D1；

    （2）求.

    【解析】（1）证明线面垂直，需要证明直线垂直这个平面内的两条相交直线，本题只需证：即可.

    （2）可以利用向量法，也可以根据平面A1ACC1与平面AB1D1垂直，可知取B1D1的中点E，则就是直线AC与平面AB1D1所成的角.然后解三角形即可.

     

    查看答案和解析>>

    1.D

    2.C 提示：画出满足条件A∪B=A∪C的文氏图，可知有五种情况，以观察其中一种，如图，显然只要图中阴影部分相等，B、C未必要相等，条件A∪B=A∪C仍可满足，对照四个选择支，A、B、D均可排除，故选C.

    3.D

    4.B 提示：由题意知，Ｍ，Ｎ，因此，（），又A∩Ｂ＝，故集合Ａ、Ｂ的子集中没有相同的集合，可知Ｍ、Ｎ中没有其他的公共元素，故正确的答案是M∩N＝.

    5．A   提示：由得，当时，△，

    得，当时，△，且，即

    所以

    6.A      7.D      8.A

    9.D提示：设3x2－4x－32＜0的一个必要不充分条件是为Q，P=.由题意知：P能推出Q，但Q不能推出P.也可理解为：PQ.

    10.A          11.B

    12.D    提示：由，又因为是的充分而不必要条件，所以，即。可知A=或方程的两根要在区间[1，2]内，也即以下两种情况：

    （1）；

    （2） ；综合（1）、（2）可得。

    二、填空题

    13.3              14.     w.w.w.k.s.5.u.c.o.m

    15. -2≤x≤6 提示：由[x]2-3[x]-10≤0得-2≤[x] ≤5，则-2≤x≤6.        16. ①④


    同步练习册答案