
题目列表(包括答案和解析)
中学数学中存在许多关系,比如“相等关系”、“平行关系”等等.如果集合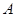 中元素之间的一个关系“
中元素之间的一个关系“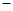 ”满足以下三个条件:
”满足以下三个条件:
(1)自反性:对于任意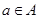 ,都有
,都有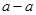 ;
;
(2)对称性:对于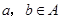 ,若
,若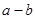 ,则有
,则有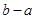 ;
;
(3)传递性:对于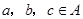 ,若
,若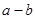 ,
,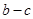 ,则有
,则有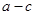 .
.
则称“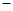 ”是集合
”是集合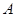 的一个等价关系.例如:“数的相等”是等价关系,而“直线的平行”不是等价关系(自反性不成立).请你再列出三个等价关系:______.
的一个等价关系.例如:“数的相等”是等价关系,而“直线的平行”不是等价关系(自反性不成立).请你再列出三个等价关系:______.
(1)自反性:对于任意a∈A,都有a~a;
(2)对称性:对于a,b∈A,若a~b,则有b~a;
(3)传递性:对于a,b,c∈A,若a~b,b~c,则有a~c.
则称“~”是集合A的一个等价关系.例如:“数的相等”是等价关系,而“直线的平行”不是等价关系(自反性不成立).请你再列出两个等价关系: .
(07年福建卷)中学数学中存在许多关系,比如“相等关系”、“平行关系”等等.如果集合A中元素之间的一个关系“-”满足以下三个条件:
(1)自反性:对于任意a∈A,都有a-a;
(2)对称性:对于a,b∈A,若a-b,则有b-a;
(3)传递性:对于a,b,c∈A,若a-b,b-c,则有a-c.
则称“-”是集合A的一个等价关系.例如:“数的相等”是等价关系,而“直线的平行”不是等价关系(自反性不成立).请你再列出两个等价关系: .
1.D

 2.C 提示:画出满足条件A∪B=A∪C的文氏图,可知有五种情况,以观察其中一种,如图,显然只要图中阴影部分相等,B、C未必要相等,条件A∪B=A∪C仍可满足,对照四个选择支,A、B、D均可排除,故选C.
2.C 提示:画出满足条件A∪B=A∪C的文氏图,可知有五种情况,以观察其中一种,如图,显然只要图中阴影部分相等,B、C未必要相等,条件A∪B=A∪C仍可满足,对照四个选择支,A、B、D均可排除,故选C.
3.D
4.B 提示:由题意知, M,
M, N,因此,
N,因此, (
( ),又A∩B=
),又A∩B= ,故集合A、B的子集中没有相同的集合,可知M、N中没有其他的公共元素,故正确的答案是M∩N=
,故集合A、B的子集中没有相同的集合,可知M、N中没有其他的公共元素,故正确的答案是M∩N= .
.
5.A 提示:由 得
得 ,当
,当 时,△
时,△ ,
,
得 ,当
,当 时,△
时,△ ,且
,且 ,即
,即
所以
6.A 7.D 8.A
9.D提示:设3x2-4x-32<0的一个必要不充分条件是为Q,P= .由题意知:P能推出Q,但Q不能推出P.也可理解为:P
.由题意知:P能推出Q,但Q不能推出P.也可理解为:P Q.
Q.
10.A 11.B
12.D 提示:由 ,又因为
,又因为 是
是 的充分而不必要条件,所以
的充分而不必要条件,所以 ,即
,即 。可知A=
。可知A= 或方程
或方程 的两根要在区间[1,2]内,也即以下两种情况:
的两根要在区间[1,2]内,也即以下两种情况:
(1) ;
;
 (2)
(2)
 ;综合(1)、(2)可得
;综合(1)、(2)可得 。
。
二、填空题
13.3 14.
 w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m
15. -2≤x≤6 提示:由[x]2-3[x]-10≤0得-2≤[x] ≤5,则-2≤x≤6. 16. ①④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com