
题目列表(包括答案和解析)
x-
| ||
| s |
| x |
(2012•湛江二模)通过随机询问110名大学生是否爱好某项运动,得到如下的列联表:
|
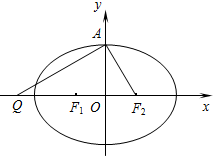 设椭圆C:
设椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| F1F2 |
| F2Q |
| 3 |
| MG |
| MH |
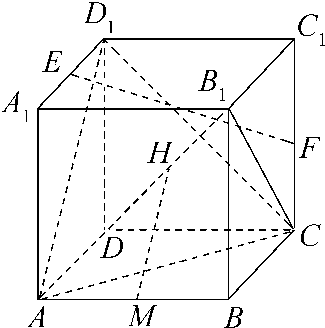 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F、M、H分别为A1D1、CC1、AB、DB1的中点.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F、M、H分别为A1D1、CC1、AB、DB1的中点.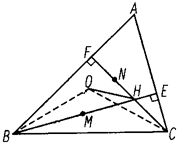 (2008•南京模拟)选修4-1:几何证明选讲
(2008•南京模拟)选修4-1:几何证明选讲| MH+NH | OH |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com