
题目列表(包括答案和解析)
已知数列 是首项为
是首项为 的等比数列,且满足
的等比数列,且满足
 .
.
(1) 求常数 的值和数列
的值和数列 的通项公式;
的通项公式;
(2) 若抽去数列 中的第一项、第四项、第七项、……、第
中的第一项、第四项、第七项、……、第 项、……,余下的项按原来的顺序组成一个新的数列
项、……,余下的项按原来的顺序组成一个新的数列 ,试写出数列
,试写出数列 的通项公式;
的通项公式;
(3) 在(2)的条件下,设数列 的前
的前 项和为
项和为 .是否存在正整数
.是否存在正整数 ,使得
,使得 ?若存在,试求所有满足条件的正整数
?若存在,试求所有满足条件的正整数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【解析】第一问中解:由 得
得 ,,
,,
又因为存在常数p使得数列 为等比数列,
为等比数列,
则 即
即 ,所以p=1
,所以p=1
故数列 为首项是2,公比为2的等比数列,即
为首项是2,公比为2的等比数列,即 .
.
此时 也满足,则所求常数
也满足,则所求常数 的值为1且
的值为1且
第二问中,解:由等比数列的性质得:
(i)当 时,
时, ;
;
(ii) 当 时,
时, ,
,
所以
第三问假设存在正整数n满足条件,则 ,
,
则(i)当 时,
时,
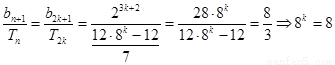
 ,
,
已知函数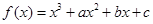 在
在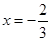 与
与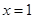 时都取得极值.
时都取得极值.
(1)求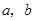 的值及函数
的值及函数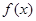 的单调区间;www.7caiedu.cn
的单调区间;www.7caiedu.cn
(2)若对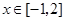 ,不等式
,不等式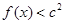 恒成立,求
恒成立,求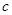 的取值范围.
的取值范围.
【解析】根据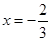 与
与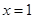 是
是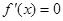 的两个根,可求出a,b的值,然后利用导数确定其单调区间即可.
的两个根,可求出a,b的值,然后利用导数确定其单调区间即可.
(2)此题本质是利用导数其函数f(x)在区间[-1,2]上的最大值,然后利用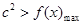 ,即可解出c的取值范围.
,即可解出c的取值范围.
当0<x≤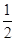 时,4x<logax,则a的取值范围是
时,4x<logax,则a的取值范围是
(A)(0,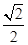 )
(B)(
)
(B)(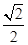 ,1) (C)(1,
,1) (C)(1,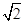 ) (D)(
) (D)(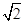 ,2)
,2)
【解析】当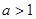 时,显然不成立.若
时,显然不成立.若 时
时
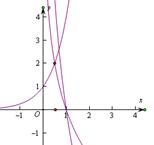
当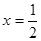 时,
时,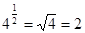 ,此时对数
,此时对数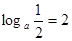 ,解得
,解得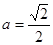 ,根据对数的图象和性质可知,要使
,根据对数的图象和性质可知,要使 在
在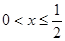 时恒成立,则有
时恒成立,则有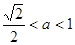 ,如图选B.
,如图选B.
设椭圆 (常数
(常数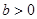 )的左右焦点分别为
)的左右焦点分别为 ,
, 是直线
是直线 上的两个动点,
上的两个动点, .
.
(1)若 ,求
,求 的值;
的值;
(2)求 的最小值.
的最小值.

【解析】第一问中解:设 ,
, 则
则
由 得
得 由
由 ,得
,得
 ②
②

第二问易求椭圆 的标准方程为:
的标准方程为:
 ,
,
所以,当且仅当 或
或 时,
时, 取最小值
取最小值 .
.
解:设 ,
, ……………………1分
……………………1分
则 ,由
,由 得
得 ①……2分
①……2分
(1)由 ,得
,得 ② ……………1分
② ……………1分
 ③ ………………………1分
③ ………………………1分
由①、②、③三式,消去 ,并求得
,并求得 .
………………………3分
.
………………………3分
(2)解法一:易求椭圆 的标准方程为:
的标准方程为: .………………2分
.………………2分
 , ……4分
, ……4分
所以,当且仅当 或
或 时,
时, 取最小值
取最小值 .…2分
.…2分
解法二: ,
………………4分
,
………………4分
所以,当且仅当 或
或 时,
时, 取最小值
取最小值
已知在等比数列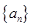 中,
中,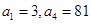 ,若数列
,若数列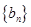 满足:
满足: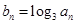 ,数列
,数列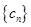 满足:
满足: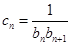 ,且数列
,且数列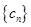 的前
的前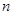 项和为
项和为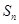 .
.
(1)求数列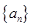 的通项公式; (2)求数列
的通项公式; (2)求数列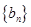 的通项公式; (3) 求
的通项公式; (3) 求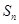 .
.
【解析】第一问∵ 在等比数列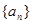 中,
中,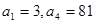 , ∴
, ∴ 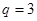
∴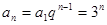
(2)中 ∵ 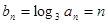
(3)中 由(2)可得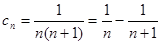 列项求和得到。
列项求和得到。
∴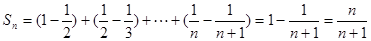
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com