
题目列表(包括答案和解析)
当实数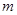 取何值时,复数
取何值时,复数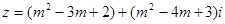 (其中
(其中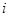 是虚数单位).
是虚数单位).
(1)是实数;(2)是纯虚数;(3)等于零.
【解析】(1)根据实数的等价条件:复数的虚部为零,列出方程求出m的值;
(2)根据纯虚数的等价条件:复数的虚部不为零、实部为零,列出方程求出m的值;
(3)根据实部和虚部都为零,列出方程求出m的值.
椭圆 的左、右焦点分别为
的左、右焦点分别为 ,一条直线
,一条直线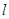 经过点
经过点 与椭圆交于
与椭圆交于 两点.
两点.
⑴求 的周长;
的周长;
⑵若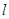 的倾斜角为
的倾斜角为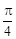 ,求
,求 的面积.
的面积.
【解析】(1)根据椭圆的定义 的周长等于4a.
的周长等于4a.
(2)设 ,则
,则 ,然后直线l的方程与椭圆方程联立,消去x,利用韦达定理可求出所求三角形的面积.
,然后直线l的方程与椭圆方程联立,消去x,利用韦达定理可求出所求三角形的面积.
已知函数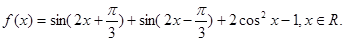
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
【解析】(1)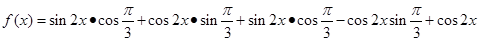
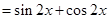
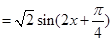 所以,
所以, 的最小正周期
的最小正周期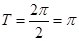
(2)因为 在区间
在区间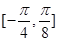 上是增函数,在区间
上是增函数,在区间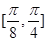 上是减函数,
上是减函数,
又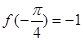 ,
,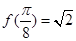 ,
,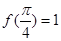 ,
,
故函数 在区间
在区间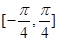 上的最大值为
上的最大值为 ,最小值为-1.
,最小值为-1.
已知 是等差数列,其前n项和为Sn,
是等差数列,其前n项和为Sn, 是等比数列,且
是等比数列,且 ,
, .
.
(Ⅰ)求数列 与
与 的通项公式;
的通项公式;
(Ⅱ)记 ,
, ,证明
,证明 (
( ).
).
【解析】(1)设等差数列 的公差为d,等比数列
的公差为d,等比数列 的公比为q.
的公比为q.
由 ,得
,得 ,
, ,
, .
.
由条件,得方程组 ,解得
,解得
所以 ,
, ,
, .
.
(2)证明:(方法一)
由(1)得
 ①
①
 ②
②
由②-①得



而
故 ,
,
(方法二:数学归纳法)
① 当n=1时,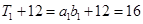 ,
, ,故等式成立.
,故等式成立.
② 假设当n=k时等式成立,即 ,则当n=k+1时,有:
,则当n=k+1时,有:






即 ,因此n=k+1时等式也成立
,因此n=k+1时等式也成立
由①和②,可知对任意 ,
, 成立.
成立.
如图,已知点 ,圆
,圆 是以
是以 为直径的圆,直线
为直径的圆,直线 ,(
,( 为参数).
为参数).
(1)以坐标原点为极点, 轴正半轴为极轴,建立极坐标系,求圆
轴正半轴为极轴,建立极坐标系,求圆 的极坐标方程;
的极坐标方程;
(2)过原点 作直线
作直线 的垂线,垂足为
的垂线,垂足为 ,若动点
,若动点 满足
满足 ,当
,当 变化时,求点
变化时,求点 轨迹的参数方程,并指出它是什么曲线.
轨迹的参数方程,并指出它是什么曲线.

【解析】(1)圆C的普通方程为
 , (2’)
, (2’)
极坐标方程为 。
(4’)
。
(4’)
(2)直线l的普通方程为 ,
(5’)
,
(5’)
点 (7’)
(7’)
 (9’)
(9’)
点M轨迹的参数方程为 ,图形为圆
,图形为圆
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com