
题目列表(包括答案和解析)
已知函数 ,
, ,k为非零实数.
,k为非零实数.
(Ⅰ)设t=k2,若函数f(x),g(x)在区间(0,+∞)上单调性相同,求k的取值范围;
(Ⅱ)是否存在正实数k,都能找到t∈[1,2],使得关于x的方程f(x)=g(x)在[1,5]上有且仅有一个实数根,且在[-5,-1]上至多有一个实数根.若存在,请求出所有k的值的集合;若不存在,请说明理由.
【解析】本试题考查了运用导数来研究函数的单调性,并求解参数的取值范围。与此同时还能对于方程解的问题,转化为图像与图像的交点问题来长处理的数学思想的运用。
(本题满分12分)
某简谐运动的图像对应的函数解析式为:![]() .
.
(1)指出此简谐运动的周期、振幅、频率、相位和初相;
(2)利用“五点法”作出函数在一个周期(闭区间)上的简图;
(3)说明它是由函数y=sinx的图像经过哪些变换而得到的。
【解】:(1)周期: ; 振幅: ;
频率: ; 相位: ;初相: ;
|
| |||||
| | 0 | ||||
|
| |||||
| |
(2)

(3)① 先将函数![]() 的图像 得到函数
的图像 得到函数
![]() 的图像;② 再将函数
的图像;② 再将函数![]() 的图像 得到
的图像 得到
函数![]() 的图像;③ 最后再将函数
的图像;③ 最后再将函数![]() 的图像
的图像
得到函数![]() 的图像。
的图像。
已知函数f(x)(x∈R)满足f(x)= ,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
(1)求函数f(x)的表达式;
(2)若数列{an}满足a1= ,an+1=f(an),bn=
,an+1=f(an),bn= -1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
-1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
(3)在(2)的条件下,证明:a1b1+a2b2+…+anbn<1(n∈N*).
【解析】解: (1)由f(x)= ,f(1)=1,得a=2b+1.
,f(1)=1,得a=2b+1.
由f(x)=2x只有一解,即 =2x,
=2x,
也就是2ax2-2(1+b)x=0(a≠0)只有一解,
∴b=-1.∴a=-1.故f(x)= .…………………………………………4分
.…………………………………………4分
(2)an+1=f(an)= (n∈N*),bn=
(n∈N*),bn= -1, ∴
-1, ∴ =
= =
= =
= ,
,
∴{bn}为等比数列,q= .又∵a1=
.又∵a1= ,∴b1=
,∴b1= -1=
-1= ,
,
bn=b1qn-1=
 n-1=
n-1= n(n∈N*).……………………………9分
n(n∈N*).……………………………9分
(3)证明:∵anbn=an =1-an=1-
=1-an=1- =
= ,
,
∴a1b1+a2b2+…+anbn= +
+ +…+
+…+ <
< +
+ +…+
+…+
= =1-
=1- <1(n∈N*).
<1(n∈N*).
已知函数 .(
.( )
)
(1)若 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(2)若在区间 上,函数
上,函数 的图象恒在曲线
的图象恒在曲线 下方,求
下方,求 的取值范围.
的取值范围.
【解析】第一问中,首先利用 在区间
在区间 上单调递增,则
上单调递增,则 在区间
在区间 上恒成立,然后分离参数法得到
上恒成立,然后分离参数法得到 ,进而得到范围;第二问中,在区间
,进而得到范围;第二问中,在区间 上,函数
上,函数 的图象恒在曲线
的图象恒在曲线 下方等价于
下方等价于 在区间
在区间 上恒成立.然后求解得到。
上恒成立.然后求解得到。
解:(1) 在区间
在区间 上单调递增,
上单调递增,
则 在区间
在区间 上恒成立. …………3分
上恒成立. …………3分
即 ,而当
,而当 时,
时, ,故
,故 .
…………5分
.
…………5分
所以 .
…………6分
.
…………6分
(2)令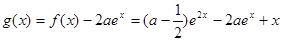 ,定义域为
,定义域为 .
.
在区间 上,函数
上,函数 的图象恒在曲线
的图象恒在曲线 下方等价于
下方等价于 在区间
在区间 上恒成立.
上恒成立.
∵ …………9分
…………9分
① 若 ,令
,令 ,得极值点
,得极值点 ,
, ,
,
当 ,即
,即 时,在(
时,在( ,+∞)上有
,+∞)上有 ,此时
,此时 在区间
在区间 上是增函数,并且在该区间上有
上是增函数,并且在该区间上有 ,不合题意;
,不合题意;
当 ,即
,即 时,同理可知,
时,同理可知, 在区间
在区间 上递增,
上递增,
有 ,也不合题意;
…………11分
,也不合题意;
…………11分
② 若 ,则有
,则有 ,此时在区间
,此时在区间 上恒有
上恒有 ,从而
,从而 在区间
在区间 上是减函数;
上是减函数;
要使 在此区间上恒成立,只须满足
在此区间上恒成立,只须满足
 ,
,
由此求得 的范围是
的范围是 . …………13分
. …………13分
综合①②可知,当 时,函数
时,函数 的图象恒在直线
的图象恒在直线 下方.
下方.
已知椭圆的中心在原点,焦点在轴上,离心率为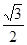 ,它与直线
,它与直线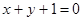 相交于P、Q两点,若
相交于P、Q两点,若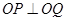 ,求椭圆方程。
,求椭圆方程。
【解析】本试题主要考查了利用椭圆的几何性质以及直线与椭圆的位置关系我们求解椭圆的方程的试题。考查了同学们运用代数的方法来解决几何问题的能力。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com