
题目列表(包括答案和解析)
如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
(1) 求证:A1C⊥平面BCDE;
(2) 若M是A1D的中点,求CM与平面A1BE所成角的大小;
(3) 线段BC上是否存在点P,使平面A1DP与平面A1BE垂直?说明理由
【解析】(1)∵ DE∥BC∴
DE∥BC∴ ∴
∴ ∴
∴ ∴
∴ 又∵
又∵ ∴
∴
(2)如图,以C为坐标原点,建立空间直角坐标系C-xyz,

则

设平面 的法向量为
的法向量为 ,则
,则 ,又
,又 ,
, ,所以
,所以 ,令
,令 ,则
,则 ,所以
,所以 ,
,
设CM与平面 所成角为
所成角为 。因为
。因为 ,
,
所以
所以CM与平面 所成角为
所成角为 。
。
| 3 |
| 5 |
| 4 |
| 5 |
| sin2α+cos2α+1 |
| 1+tanα |
| π |
| 2 |
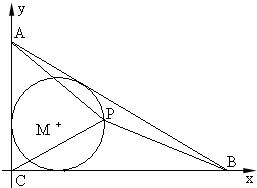 已知△ABC中,
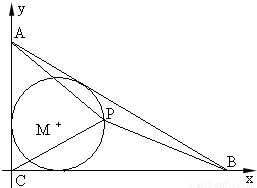
已知△ABC中,| cosA |
| cosB |
| AC |
| BC |
| 3 |
| 4 |
 如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于点P,Q,已知点P的坐标为(-
如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于点P,Q,已知点P的坐标为(-| 3 |
| 5 |
| 4 |
| 5 |
| sin2α+cos2α+1 |
| 1+tanα |
| OP |
| OQ |
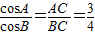 ,
,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com