如图，F是团圆＝1(a＞b＞0)的一个焦点，A、B是椭圆的两个顶点，椭圆的离心率为，点C在X轴上，BC⊥BF，B，C，F三点确定的圆M恰好与直线x＋＋3＝0相切．

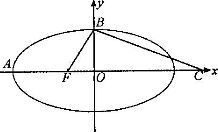
(Ⅰ)求椭圆的方程；

(Ⅱ)过F作一条与两坐标都不垂直的直线l交椭圆于P、Q两点，在x轴上是否存在点N，使得NF恰好为PNQ的内角评分线，若存在，求出点N的坐标，若不存在，请说明理由．

查看答案和解析>>

一、选择题：本题工12个小题，每小题5分，共60分。

题号

1

2

3

4

5

6

7

8

9

10

11

12

答案

D

A

A

C

D

A

B

D

B

D

C

C

二、填空题：本题供4个小题，每小题4分，工16分。

  13.        14.2       15.5       16.12

三、解答题：本题工6个小题，工74分。

17（本小题满分12分）

解：（I）

（2）由（I）知

18（本小题满分12分）

   解：（I）

       又

21.（本小题满分12分）

解：（I）由题意，，f(x)的定义域