
题目列表(包括答案和解析)
【答案】0<m<2.
【考点】二次函数的图象;反比例函数的图象.
【专题】图表型.
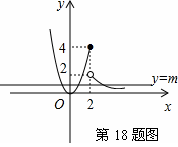
【分析】首先作出分段函数y=![]() 的图象,根据函数的图象即可确定m的取值范围.
的图象,根据函数的图象即可确定m的取值范围.
 【解答】分段函数y=
【解答】分段函数y=![]() 的图象如右图所示:
的图象如右图所示:
故要使直线y=m(m为常数)与函数y=![]() 的图象恒有三个不同的交点,常数m的取值范围为0<m<2,
的图象恒有三个不同的交点,常数m的取值范围为0<m<2,
故答案为:0<m<2.
【点评】本题考查了二次函数的图象及反比例函数的图象,首先作出分段函数的图象是解决本题的关键,采用数形结合的方法确定答案是数学上常用的方法之一.
【解题思路】(1)如下表
| 甲(s) 乙(t) | 红桃3 | 红桃4 | 黑桃5 |
| 红桃3 |
|
|
|
| 红桃4 |
|
|
|
| 黑桃5 |
|
|
|
由上表可知:︱s-t︱≥1的概率= ![]() =
=![]() (也可画树形图求解)。
(也可画树形图求解)。
(2)方案A:如表
| 甲(花色) 乙(花色) | 红桃3 | 红桃4 | 黑桃5 |
| 红桃3 | 同色 | 同色 | 不同色 |
| 红桃4 | 同色 | 同色 | 不同色 |
| 黑桃5 | 不同色 | 不同色 | 同色 |
由上表可得![]()
方案B:如表
| 甲 乙 | 红桃3 | 红桃4 | 黑桃5 |
| 红桃3 | 3+3=6 | 3+4=7 | 3+5=8 |
| 红桃4 | 4+3=7 | 4+4=8 | 4+5=9 |
| 黑桃5 | 5+3=8 | 5+4=9 | 5+5=10 |
由上表可得![]()
因为![]() ,所以选择A方案甲的胜率更高.
,所以选择A方案甲的胜率更高.
【答案】⑴![]() ⑵A方案
⑵A方案![]() ,B方案
,B方案![]() ,故选择A方案甲的胜率更高.
,故选择A方案甲的胜率更高.
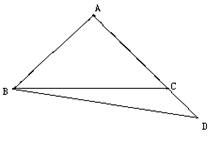
已知△ABC中,∠BAC=90°, AB=AC. (1)(5分)如图,D为AC上任一点,连接BD,过A点作BD的垂线交过C点与AB平行的直线CE于点E.求证:BD=AE.
(2)(6分) 若点D在AC的延长线上,如图,其他条件同(1),请画出此时的图形,并猜想BD与AE是否仍然相等?说明你的理由.
【解析】(1)先证∠ABD=∠CAE,再证△ABD≌△CAE即可得出答案.
(2)根据题意画出图形,然后可根据△ABD≌△ACE得出结论
已知△ABC中,∠BAC=90°, AB=AC. (1)(5分) 如图,D为AC上任一点,连接BD,过A点作BD的垂线交过C点与AB平行的直线CE于点E.求证:BD=AE.

(2)(6分) 若点D在AC的延长线上,如图,其他条件同(1),请画出此时的图形,并猜想BD与AE是否仍然相等?说明你的理由.
【解析】(1)先证∠ABD=∠CAE,再证△ABD≌△CAE即可得出答案.
(2)根据题意画出图形,然后可根据△ABD≌△ACE得出结论
如图,△ABC中,∠BAC=90°,AC=2,AB=![]() ,△ACD是等边三角形.
,△ACD是等边三角形.
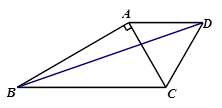
(1)求∠ABC的度数.
(2)以点A为中心,把△ABD顺时针旋转60°,
画出旋转后的图形.
(3)求BD的长度.
【解析】(1)利用正切的知识可得出答案.
(2)根据旋转角度、旋转中心、旋转方向找出各点的对称点,顺次连接即可;
(3)根据旋转的性质可得△ACE≌△ADB,从而确定∠EBC=90°,然后利用勾股定理即可解答
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com