
题目列表(包括答案和解析)
【答案】14![]() 。
。
【考点】轴对称-最短路线问题;勾股定理;垂径定理.
【专题】探究型.
【分析】先由MN=20求出⊙O的半径,再连接OA、OB,由勾股定理得出OD、OC的长,作点B关于MN的对称点B′,连接AB′,则AB′即为PA+PB的最小值,B′D=BD=6,过点B′作AC的垂线,交AC的延长线于点E,在Rt△AB′E中利用勾股定理即可求出AB′的值.
【解答】∵MN=20,
∴⊙O的半径=10,
连接OA、OB,
在Rt△OBD中,OB=10,BD=6,
∴OD=![]() =
=![]() =8;
=8;
同理,在Rt△AOC中,OA=10,AC=8,
∴OC=![]() =
=![]() =6,
=6,
∴CD=8+6=14,
作点B关于MN的对称点B′,连接AB′,则AB′即为PA+PB的最小值,B′D=BD=6,过点B′作AC的垂线,交AC的延长线于点E,
在Rt△AB′E中,
∵AE=AC+CE=8+6=14,B′E=CD=14,
∴AB′=![]() =
=![]() =14
=14![]() .
.
故答案为:14![]() .
.
【点评】本题考查的是轴对称-最短路线问题、垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.
一步合五尺.题意如图所示,AC=1(踏板一尺离地),CD=10(送行二步),BD=5(五尺人高).
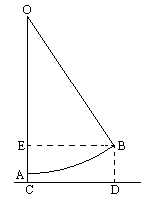
设索长OA为x尺,则在Rt△OBE中,
OB=x,BE=CD=10,
OE=OA+AC-CE=OA+AC-BD,
即 OE=x+1-5=x-4
由勾股定理得
x2=102+(x-4)2,
解得 x=14.5,
即索长一丈四尺五寸.
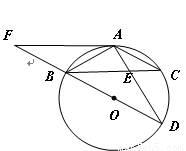
如图,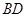 为⊙
为⊙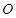 的直径,
的直径,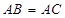 ,
,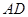 交
交 于点
于点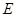 ,
,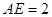 ,
,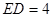 .
.
(1)求证: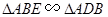 ;
;
(2)求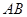 的长;
的长;
(3)延长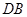 到
到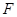 ,使得
,使得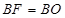 ,连接
,连接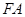 ,试判断直
线
,试判断直
线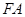 与⊙
与⊙ 的位置关系,并说明理由.
的位置关系,并说明理由.
【解析】(1)根据AB=AC,可得∠ABC=∠C,利用等量代换可得∠ABC=∠D然后即可证明△ABE∽△ADB.
(2)根据△ABE∽△ADB,利用其对应边成比例,将已知数值代入即可求得AB的长.
(3)连接OA,根据BD为⊙O的直径可得∠BAD=90°,利用勾股定理求得BD,然后再求证∠OAF=90°即可
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com