
题目列表(包括答案和解析)
已知点A、B、C的坐标分别为A(3,0)、B(0,3)、C(cosα,sinα),
α∈( ,
, ).
).
(1)若| |=|
|=| |,求角α的值;
|,求角α的值;
(2)若 ·
· =-1,求
=-1,求 的值.
的值.
【解析】第一问中利用向量的模相等,可以得到角α的值。
第二问中, ·
· =-1,则化简
=-1,则化简 可知结论为
可知结论为
解:因为点A、B、C的坐标分别为A(3,0)、B(0,3)、C(cosα,sinα),
α∈( ,
, ).|
).| |=|
|=| |
所以α=
|
所以α= .
.
(2)因为 ·
· =-1,
=-1, 即
即 .
.
已知 ,
, 是椭圆
是椭圆
 左右焦点,它的离心率
左右焦点,它的离心率 ,且被直线
,且被直线 所截得的线段的中点的横坐标为
所截得的线段的中点的横坐标为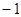
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设 是其椭圆上的任意一点,当
是其椭圆上的任意一点,当 为钝角时,求
为钝角时,求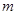 的取值范围。
的取值范围。
【解析】解:因为第一问中,利用椭圆的性质由 得
得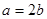 所以椭圆方程可设为:
所以椭圆方程可设为: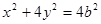 ,然后利用
,然后利用
得 得
得


 椭圆方程为
椭圆方程为
第二问中,当 为钝角时,
为钝角时, ,
得
,
得
所以 得
得
解:(Ⅰ)由 得
得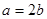 所以椭圆方程可设为:
所以椭圆方程可设为: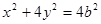
 3分
3分
得 得
得


 椭圆方程为
椭圆方程为 3分
3分
(Ⅱ)当 为钝角时,
为钝角时, ,
得
,
得 3分
3分
所以 得
得
3+
| ||
| 2 |
3-
| ||
| 2 |
3+
| ||
| 2 |
3-
| ||
| 2 |
2.A解析:由![]() 知函数在
知函数在![]() 上有零点,又因为函数在(0,+
上有零点,又因为函数在(0,+![]() )上是减函数,所以函数y=f(x) 在(0,+
)上是减函数,所以函数y=f(x) 在(0,+![]() )上有且只有一个零点不妨设为
)上有且只有一个零点不妨设为![]() ,则
,则![]() ,又因为函数是偶函数,所以
,又因为函数是偶函数,所以![]() =0并且函数在(0,+
=0并且函数在(0,+![]() )上是减函数,因此-
)上是减函数,因此-![]() 是(-
是(-![]() ,0)上的唯一零点,所以函数共有两个零点
,0)上的唯一零点,所以函数共有两个零点
下列叙述中,是随机变量的有( )
①某工厂加工的零件,实际尺寸与规定尺寸之差;②标准状态下,水沸腾的温度;③某大桥一天经过的车辆数;④向平面上投掷一点,此点坐标.
A.②③ B.①② C.①③④ D.①③
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com