【答案】60°。

【考点】平行线的性质；三角形的外角性质．

【分析】利用三角形的一个外角等于与它不相邻的两个内角的和求出∠3的同位角的度数，再根据两直线平行，同位角相等即可求解．

【解答】如图，∵∠1＝130°，∠2＝70°，

∴∠4＝∠1－∠2＝130°－70°＝60°，

∵a∥b，

∴∠3＝∠4＝60°．

故答案为：60°．

【点评】本题考查了平行线的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，准确识图，理清图中各角度之间的关系是解题的关键．

【答案】14。

【考点】轴对称-最短路线问题；勾股定理；垂径定理．

【专题】探究型．

【分析】先由MN＝20求出⊙O的半径，再连接OA、OB，由勾股定理得出OD、OC的长，作点B关于MN的对称点B′，连接AB′，则AB′即为PA＋PB的最小值，B′D＝BD＝6，过点B′作AC的垂线，交AC的延长线于点E，在Rt△AB′E中利用勾股定理即可求出AB′的值．

【解答】∵MN＝20，

∴⊙O的半径＝10，

连接OA、OB，

在Rt△OBD中，OB＝10，BD＝6，

∴OD＝＝＝8；

同理，在Rt△AOC中，OA＝10，AC＝8，

∴OC＝＝＝6，

∴CD＝8＋6＝14，

作点B关于MN的对称点B′，连接AB′，则AB′即为PA＋PB的最小值，B′D＝BD＝6，过点B′作AC的垂线，交AC的延长线于点E，

在Rt△AB′E中，

∵AE＝AC＋CE＝8＋6＝14，B′E＝CD＝14，

∴AB′＝＝＝14．

故答案为：14．

【点评】本题考查的是轴对称-最短路线问题、垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形，利用勾股定理求解是解答此题的关键．

【答案】0＜m＜2．

【考点】二次函数的图象；反比例函数的图象．

【专题】图表型．

【分析】首先作出分段函数y＝的图象，根据函数的图象即可确定m的取值范围．

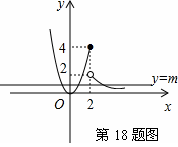【解答】分段函数y＝的图象如右图所示：

故要使直线y＝m（m为常数）与函数y＝的图象恒有三个不同的交点，常数m的取值范围为0＜m＜2，

故答案为：0＜m＜2．

【点评】本题考查了二次函数的图象及反比例函数的图象，首先作出分段函数的图象是解决本题的关键，采用数形结合的方法确定答案是数学上常用的方法之一．

已知直线L：y=-3x+2，现有命题：
①点P（-1，1）在直线L上；
②若直线L与x轴，y轴分别交于A，B两点，则AB=

2 10

3

；
③若点M（

1

3

，1），N（a，b）都在直线L上，且a＞

1

3

，则b＞1；
④若点Q到两坐标轴的距离相等，且Q在L上，则点Q在第一或第四象限，其中正确的命题是．（按照顺序填序号，答案格式如：12345）

已知直线L：y=-3x+2，现有命题：
①点P（-1，1）在直线L上；
②若直线L与x轴，y轴分别交于A，B两点，则AB=；
③若点M（，1），N（a，b）都在直线L上，且a＞，则b＞1；
④若点Q到两坐标轴的距离相等，且Q在L上，则点Q在第一或第四象限，其中正确的命题是    ．（按照顺序填序号，答案格式如：12345）