解答：由题意得：

  解得：

∴

∴，即

∴

故

解答：由题意得：且

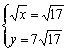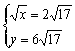∴或或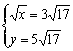

故符合条件的有3对.

由切饼想到的

　　观察是思考的“外壳”，要想思考得好，一定要善于观察．数学家在发现或解决问题时往往首先依赖于他对若干现象的观察－－通过观察，如果发现某种值得注意的规律，就对它进行研究，并力图从中发现某种结论，去解释或描述这种模型，以求问题的顺利解决．例如，如果让你用任意方法去切一块圆饼，只要通过同一点不超过两刀，那么最多能得到几块？

　　自然，我们用不着特地去买一块饼来，只要在纸上画一些圆就行了．我们对各圆进行不同次数的切割，并在表中记录结果，得到：

　　我们仔细考查一下这张表，看看能否找到其中的规律．从记录上看，增加的块数分别是自然数1，2，3．切割次数也分别是1，2，3．这种规律是否继续有效呢？让我们再多试几次，并记录数据，得到：

　　现在的增加数分别是1，2，3，4，5，可见规律继续有效．这种规律使我们预测到：切割6次得22块，切割7次得29块．并进一步能使我们预测切割任意次所得的块数．

想一想：切割8次、9次将分别得到多少块？

本题分为A、B 两类题，你可从A、B 两类题中任选一题解答即可
（A类）：如图，在△ABC中，AB=AC=a，M为底边BC上的任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q．
（1）求四边形AQMP的周长；
（2）写出图中的两对相似三角形（不需证明）；
（3）M位于BC的什么位置时，四边形AQMP为菱形？说明你的理由．
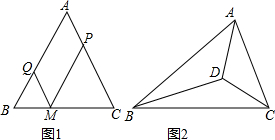（B类）：有人这样证明三角形内角和是180°，如图，D是△ABC内一点，连接AD、BD、CD，他们将△ABC分成了三个小的三角形．因此有：三个小三角形的内角和的和比△ABC的内角和多360°，如果设三角形内角和是x，则有：x+x+x=x+360°，易解得x=180°，你认为这个证明正确吗？说说你的理由．