
题目列表(包括答案和解析)
 已知:如图,抛物线y=ax2+bx+c与x轴交于点A(
已知:如图,抛物线y=ax2+bx+c与x轴交于点A(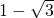 ,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P′(1,3)处.
,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P′(1,3)处. (约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据:
(约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据: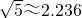 ,
,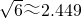 ,结果精确到0.001)
,结果精确到0.001) ,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P′(1,3)处.
,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P′(1,3)处.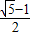 (约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据:
(约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据: ,
, ,结果精确到0.001)
,结果精确到0.001)
(本题满分9分)
如图,以为顶点的抛物线与
轴交于点
.已知
、
两点坐标分别为(3,0)、(0,4).
(1)求抛物线的解析式;
(2)设是抛物线上的一点(
、
为正整数),且它位于对称轴的右侧.若以
、
、
、
为顶点的四边形四条边的长度是四个连续的正整数,求点
的坐标;
(3)在(2)的条件下,试问:对于抛物线对称轴上的任意一点,
![]() 是否总成立?请说明理由.
是否总成立?请说明理由.
 为顶点的抛物线与
为顶点的抛物线与 轴交于点
轴交于点 .已知
.已知 、
、 两点坐标分别为(3,0)、(0,4).
两点坐标分别为(3,0)、(0,4). 是抛物线上的一点(
是抛物线上的一点( 、
、 为正整数),且它位于对称轴的右侧.若以
为正整数),且它位于对称轴的右侧.若以 、
、 、
、 、
、 为顶点的四边形四条边的长度是四个连续的正整数,求点
为顶点的四边形四条边的长度是四个连续的正整数,求点 的坐标;
的坐标;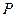 ,
, 是否总成立?请说明理由.
是否总成立?请说明理由.
(本题满分9分)
如图,以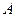 为顶点的抛物线与
为顶点的抛物线与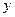 轴交于点
轴交于点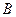 .已知
.已知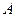 、
、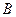 两点坐标分别为(3,0)、(0,4).
两点坐标分别为(3,0)、(0,4).
(1)求抛物线的解析式;
(2)设 是抛物线上的一点(
是抛物线上的一点(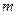 、
、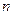 为正整数),且它位于对称轴的右侧.若以
为正整数),且它位于对称轴的右侧.若以 、
、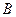 、
、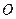 、
、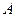 为顶点的四边形四条边的长度是四个连续的正整数,求点
为顶点的四边形四条边的长度是四个连续的正整数,求点 的坐标;
的坐标;
(3)在(2)的条件下,试问:对于抛物线对称轴上的任意一点 ,
,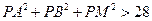 是否总成立?请说明理由.
是否总成立?请说明理由.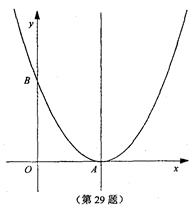
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com