
题目列表(包括答案和解析)
 ,且CB=CE.
,且CB=CE. 19、如图,①AB=DE、②CB=CE、③∠1=∠2、④CA=CD.请从中选出三个作为条件,一个作为结论,写出所有成立的命题,并选择其中一个加以证明.
19、如图,①AB=DE、②CB=CE、③∠1=∠2、④CA=CD.请从中选出三个作为条件,一个作为结论,写出所有成立的命题,并选择其中一个加以证明.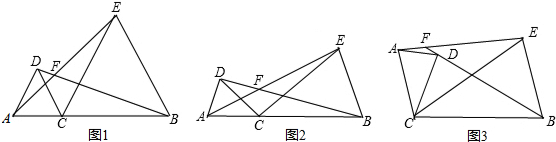
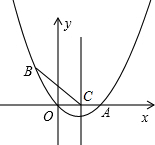 (2,0).
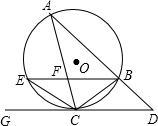
(2,0). (2012•武汉模拟)如图,AB为⊙O的直径,AM和BN是它的两条切线,E为⊙O的半圆弧上一动点(不与A、B重合),过点E的直线分别交射线AM、BN于D、C两点,且CB=CE.
(2012•武汉模拟)如图,AB为⊙O的直径,AM和BN是它的两条切线,E为⊙O的半圆弧上一动点(不与A、B重合),过点E的直线分别交射线AM、BN于D、C两点,且CB=CE.
| ||
| 2 |
| AH |
| CH |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com