
题目列表(包括答案和解析)
 万吨•千米)尽可能小.
万吨•千米)尽可能小.| 地区 水库 |
甲 | 乙 | 总计 |
| A | x | 14-x 14-x |
14 |
| B | 15-x 15-x |
x-1 x-1 |
14 |
| 总计 | 15 | 13 | 28 |
|
|
| x |
| -x |
| x |
| -x |
|
| x2-1 |
| 1-x2 |
| x-2 |
| 2-x |
| x |
| -x |
| x |
| -x |
|
| x2-1 |
| 1-x2 |
| x-2 |
| 2-x |
 有意义,则x≥0;式子
有意义,则x≥0;式子 有意义,则x≤0;若式子
有意义,则x≤0;若式子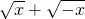 有意义,求x的取值范围;这个问题可以转化为不等式组来解决,即求关于x的不等式组
有意义,求x的取值范围;这个问题可以转化为不等式组来解决,即求关于x的不等式组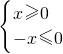 的解集,解这个不等式组得x=0.请你运用上述的数学方法解决下列问题:
的解集,解这个不等式组得x=0.请你运用上述的数学方法解决下列问题: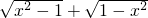 有意义,求x的取值范围;
有意义,求x的取值范围;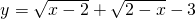 ,求xy的值.
,求xy的值.
|
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com