
题目列表(包括答案和解析)
| 7 |
| 9 |
| 19a |
| 72 |
| 7 |
| 9 |
| 19 |
| 72 |
(1)求an的表达式;
(2)为保护生态环境,防止水土流失,该地区每年的森林木材量应不少于![]() a,如果b=
a,如果b=![]() a,那么该地区今后会发生水土流失吗?若会,需要经过几年?(取lg2=0.30).
a,那么该地区今后会发生水土流失吗?若会,需要经过几年?(取lg2=0.30).
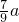 ,如果
,如果 ,那么该地区今后会发生水土流失吗?若会,需要经过几年?(参考数据:lg2=0.3)
,那么该地区今后会发生水土流失吗?若会,需要经过几年?(参考数据:lg2=0.3)湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com