已知数列{a_n}中，a₁＝1，a₂＝3且2a_n＋1＝a_n＋2＋a_n（n∈N^*）．数列{b_n}的前n项和为S_n，其中b₁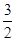＝－，b_n＋1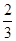＝－S_n（n∈N^*）．

（1）求数列{a_n}和{b_n}的通项公式；

（2）若T_n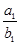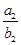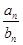＝＋＋…＋，求T_n的表达式．

已知函数f(x)(x∈R)满足f(x)＝，a≠0，f(1)＝1，且使f(x)＝2x成立的实数x只有一个．

(1)求函数f(x)的表达式；

(2)若数列{a_n}满足a₁＝，a_n+1＝f(a_n)，b_n＝－1，n∈N^*，证明数列{b_n}是等比数列，并求出{b_n}的通项公式；

(3)在(2)的条件下，证明：a₁b₁＋a₂b₂＋…＋a_nb_n<1(n∈N^*)．

【解析】解： (1)由f(x)＝，f(1)＝1，得a＝2b＋1.

由f(x)＝2x只有一解，即＝2x，

也就是2ax²－2(1＋b)x＝0(a≠0)只有一解，

∴b＝－1.∴a＝－1.故f(x)＝.…………………………………………4分

(2)a_n＋1＝f(a_n)＝(n∈N^*)，b_n＝－1， ∴＝＝＝，

∴{b_n}为等比数列，q＝.又∵a₁＝，∴b₁＝－1＝，

b_n＝b₁q^n－1＝^n－1＝ⁿ(n∈N^*)．……………………………9分

(3)证明：∵a_nb_n＝a_n＝1－a_n＝1－＝，

∴a₁b₁＋a₂b₂＋…＋a_nb_n＝＋＋…＋<＋＋…＋

＝＝1－<1(n∈N^*)．

数列{a_n}中，a₁＝8，a₄＝2且满足a_n＋2＝2a_n＋1－a_n  n∈N

（1）求数列{a_n}的通项公式；

（2）设S_n＝|a₁|＋|a₂|＋…＋|a_n|，求s_n;

（3）设b_n＝ ( n∈N)，T_n＝b₁＋b₂＋…＋b_n( n∈N)，是否存在最大的整数m，使得对任意n∈N，均有T_n＞成立？若存在，求出m的值；若不存在，请说明理由。

设数列{a_n}的前n项和为S_n＝2n²，{b_n}为等比数列，且a₁＝b₁，b₁(a₂－a₁)＝b₂.

(1)求数列{a_n}和{b_n}的通项公式；

(2)设c_n＝a_n b_n，求数列{c_n}的前n项和T_n.

数列{a_n}中，a₁＝8，a₄＝2且满足a_n＋2＝2a_n＋1－a_n  n∈N

（1）求数列{a_n}的通项公式；

（2）设S_n＝|a₁|＋|a₂|＋…＋|a_n|，求s_n;

（3）设b_n＝ ( n∈N)，T_n＝b₁＋b₂＋…＋b_n( n∈N)，是否存在最大的整数m，使得对任意n∈N，均有T_n＞成立？若存在，求出m的值；若不存在，请说明理由。