
题目列表(包括答案和解析)
阅读下列材料并填空。平面上有n个点(n≥2)且任意三个点不在同一条直线上,过这些点作直线,一共能作出多少条不同的直线?
(1)分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线……
(2)归纳:考察点的个数和可连成直线的条数 发现:如下表
发现:如下表
|
点的个数 |
可作出直线条数 |
|
2 |
1= |
|
3 |
3= |
|
4 |
6= |
|
5 |
10= |
|
…… |
…… |
|
n |
|
(3)推理:平面上有n个点,两点确定一条直线。取第一个点A有n种取法,取第二个点B有(n-1)种取法,所以一共可连成n(n-1)条直线,但AB与BA是同一条直线,故应除以2;即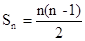
(4)结论: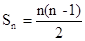
试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
(1)分析:
当仅有3个点时,可作出 个三角形;
当仅有4个点时,可作出 个三角形;
当仅有5个点时,可作出 个三角形;
……
(2)归纳:考察点的个数n和可作出的三角形的个数 ,发现:(填下表)
,发现:(填下表)
|
点的个数 |
可连成三角形个数 |
|
3 |
|
|
4 |
|
|
5 |
|
|
…… |
|
|
n |
|
(3)推理: (4)结论:
、阅读下列材料并填空。平面上有n个点(n≥2)且任意三个点不在同一条直线上,过这些点作直线,一共能作出多少条不同的直线?
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线……
②归纳:考察点的个数和可连成直线的条数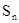 发现:如下表
发现:如下表
|
点的个数 |
可作出直线条数 |
|
2 |
1= |
|
3 |
3= |
|
4 |
6= |
|
5 |
10= |
|
…… |
…… |
|
n |
|
③推理:平面上有n个点,两点确定一条直线。取第一个点A有n种取法,取第二个点B有(n-1)种取法,所以一共可连成n(n-1)条直线,但AB与BA是同一条直线,故应除以2;即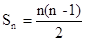
④结论: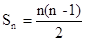
试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
(1)分析:
当仅有3个点时,可作出 个三角形;
当仅有4个点时,可作出 个三角形;
当仅有5个点时,可作出 个三角形;
……
(2)归纳:考察点的个数n和可作出的三角形的个数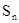 ,发现:(填下表)
,发现:(填下表)
|
点的个数 |
可连成三角形个数 |
|
3 |
|
|
4 |
|
|
5 |
|
|
…… |
|
|
n |
|
(3)推理:
(4)结论:
| 点的个数 | 可作出直线条数 |
| 2 | 1=S2= |
| 3 | 3=S3= |
| 4 | 6=S4= |
| 5 | 10=S5=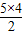 |
| … | … |
| n | Sn= |
 ④结论:Sn=
④结论:Sn= 试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?| 点的个数 | 可连成三角形个数 |
| 3 | |
| 4 | |
| 5 | |
| … | |
| n |
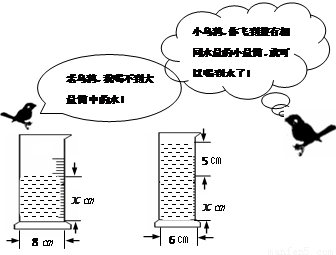
如图2,
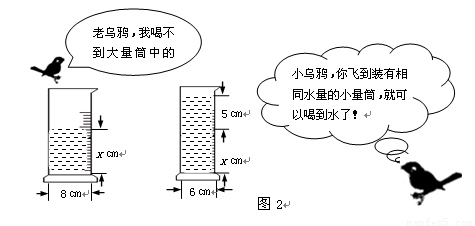
请根据图中给出的信息,可得正确的方程是( )
A、π×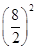 x=π×
x=π×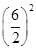 ×(x+5) B、π×
×(x+5) B、π×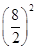 x=π×
x=π×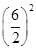 ×(x-5)
×(x-5)
C、π×82×x=π×62×(x+5) D、π×82×x=π×62×5
请根据图中给出的信息,可得正确的方程是( )
A.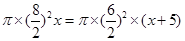
B.
C.
D.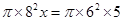
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com