
题目列表(包括答案和解析)
| 1 |
| 3 |
| 1 |
| 4 |
列方程(组)解应用题:
为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场. 现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
 S梯形ABCD?若存在,求出t值.若不存在,说明理由.
S梯形ABCD?若存在,求出t值.若不存在,说明理由.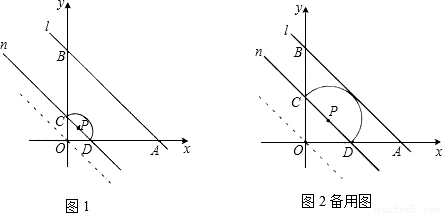
 S梯形ABCD?若存在,求出t值.若不存在,说明理由.
S梯形ABCD?若存在,求出t值.若不存在,说明理由.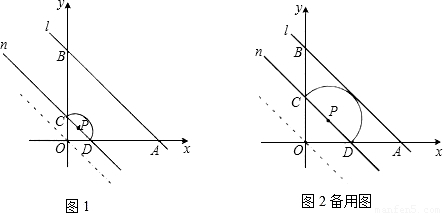
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com