（2013•闵行区一模）如图，对大于或等于2的正整数m的n次幂进行如下方式的“分裂”（其中m、n∈N^*）：例如7²的“分裂”中最小的数是1，最大的数是13；若m³的“分裂”中最小的数是211，则m=．

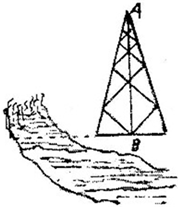（2012•包头一模）如图，AB是底部B不可到达的一个塔型建筑物，A为塔的最高点．现需在对岸测出塔高AB，甲、乙两同学各提出了一种测量方法，甲同学的方法是：选与塔底B在同一水平面内的一条基线CD，使C，D，B三点不在同一条直线上，测出∠DCB及∠CDB的大小（分别用α，β表示测得的数据）以及C，D间的距离（用s表示测得的数据），另外需在点C测得塔顶A的仰角（用θ表示测量的数据），就可以求得塔离AB．乙同学的方法是：选一条水平基线EF，使E，F，B三点在同一条直线上．在E，F处分别测得塔顶A的仰角（分别用α，β表示测得的数据）以及E，F间的距离（用s表示测得的数据），就可以求得塔高AB．
请从甲或乙的想法中选出一种测量方法，写出你的选择并按如下要求完成测量计算：
①画出测量示意图；
②用所叙述的相应字母表示测量数据，画图时C，D，B按顺时针方向标注，E，F按从左到右的方向标注；
③求塔高AB．

（2013•绵阳二模）设m是一个正整数，对两个正整数a、b，若a-b=km（k∈Z，k≠0），我们称a、b模m同余，用符号a=b（Modm）表示； 在6=b（Modm）中，当

b

m

∈N，且m＞1时，b的所有可取值为．