
题目列表(包括答案和解析)
(本大题18分)
阅读下面所给材料:已知数列{an},a1=2,an=3an–1+2,求数列的通项an。
解:令an=an–1=x,则有x=3x+2,所以x= –1,故原递推式an=3an–1+2可转化为:
an+1=3(an–1+1),因此数列{an+1}是首项为a1+1,公比为3的等比数列。
根据上述材料所给出提示,解答下列问题:
已知数列{an},a1=1,an=3an–1+4,
(1)求数列的通项an;并用解析几何中的有关思想方法来解释其原理;
(2)若记Sn=![]() ,求
,求![]() Sn;
Sn;
(3)若数列{bn}满足:b1=10,bn+1=100![]() ,利用所学过的知识,把问题转化为可以用阅读材料的提示,求出解数列{bn}的通项公式bn。
,利用所学过的知识,把问题转化为可以用阅读材料的提示,求出解数列{bn}的通项公式bn。
(本题满分16分,第1小题 4分,第2小题6分,第3小题6分)
设函数![]() ,数列
,数列![]() 满足
满足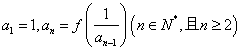 .
.
⑴求数列![]() 的通项公式;
的通项公式;
⑵设![]() ,若
,若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
⑶是否存在以![]() 为首项,公比为
为首项,公比为![]() 的数列
的数列![]() ,
,![]() ,使得数列
,使得数列![]() 中每一项都是数列
中每一项都是数列![]() 中不同的项,若存在,求出所有满足条件的数列
中不同的项,若存在,求出所有满足条件的数列![]() 的通项公式;若不存在,说明理由.
的通项公式;若不存在,说明理由.
(本题满分16分,第1小题 4分,第2小题6分,第3小题6分)
设函数![]() ,数列
,数列![]() 满足
满足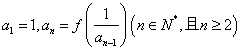 .
.
⑴求数列![]() 的通项公式;
的通项公式;
⑵设![]() ,若
,若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
⑶是否存在以![]() 为首项,公比为
为首项,公比为![]() 的数列
的数列![]() ,
,![]() ,使得数列
,使得数列![]() 中每一项都是数列
中每一项都是数列![]() 中不同的项,若存在,求出所有满足条件的数列
中不同的项,若存在,求出所有满足条件的数列![]() 的通项公式;若不存在,说明理由.
的通项公式;若不存在,说明理由.
(本题满分16分,第1小题4分,第2小题6分,第3小题6分)
设函数![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() (
(![]() ∈N*,且
∈N*,且![]() ≥2)。
≥2)。
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,若
,若![]() ≥
≥![]() 对
对![]() ∈N*恒成立,求实数
∈N*恒成立,求实数![]() 的取值范围;
的取值范围;
(3)是否存在以![]() 为首项,公比为
为首项,公比为![]() (
(![]() )的数列
)的数列![]() ,
,![]() ,使得数列
,使得数列![]() 中的每一项都是数列
中的每一项都是数列![]() 中不同的项,若存在,求出所有满足条件的数列
中不同的项,若存在,求出所有满足条件的数列![]() 的通项公式;若不存在,说明理由。
的通项公式;若不存在,说明理由。
(本题满分16分,第1小题4分,第2小题6分,第3小题6分)
设函数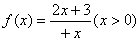 ,数列
,数列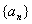 满足
满足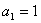 ,
,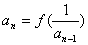 (
(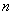 ∈N*,且
∈N*,且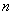 ≥2)。
≥2)。
(1)求数列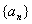 的通项公式;
的通项公式;
(2)设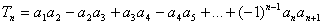 ,若
,若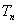 ≥
≥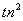 对
对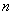 ∈N*恒成立,求实数
∈N*恒成立,求实数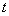 的取值范围;
的取值范围;
(3)是否存在以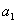 为首项,公比为
为首项,公比为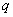 (
(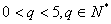 )的数列
)的数列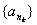 ,
,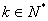 ,使得数列
,使得数列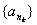 中的每一项都是数列
中的每一项都是数列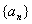 中不同的项,若存在,求出所有满足条件的数列
中不同的项,若存在,求出所有满足条件的数列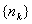 的通项公式;若不存在,说明理由。
的通项公式;若不存在,说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com