
题目列表(包括答案和解析)
设A是如下形式的2行3列的数表,
|
a |
b |
c |
|
d |
e |
f |
满足性质P:a,b,c,d,e,f ,且a+b+c+d+e+f=0
,且a+b+c+d+e+f=0
记 为A的第i行各数之和(i=1,2),
为A的第i行各数之和(i=1,2),  为A的第j列各数之和(j=1,2,3)记
为A的第j列各数之和(j=1,2,3)记 为
为 中的最小值。
中的最小值。
(1)对如下表A,求 的值
的值
|
1 |
1 |
-0.8 |
|
0.1 |
-0.3 |
-1 |
(2)设数表A形如
|
1 |
1 |
-1-2d |
|
d |
d |
-1 |
其中 ,求
,求 的最大值
的最大值
(3)对所有满足性质P的2行3列的数表A,求 的最大值。
的最大值。
【解析】(1)因为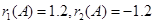 ,
, ,所以
,所以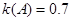
(2)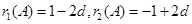 ,
,
因为 ,所以
,所以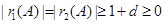 ,
,
所以
当d=0时, 取得最大值1
取得最大值1
(3)任给满足性质P的数表A(如图所示)
|
a |
b |
c |
|
d |
e |
f |
任意改变A的行次序或列次序,或把A中的每个数换成它的相反数,所得数表 仍满足性质P,并且
仍满足性质P,并且 ,因此,不妨设
,因此,不妨设 ,
, ,
,
由 得定义知,
得定义知, ,
, ,
, ,
,
从而

所以, ,由(2)知,存在满足性质P的数表A使
,由(2)知,存在满足性质P的数表A使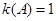 ,故
,故 的最大值为1
的最大值为1
【考点定位】此题作为压轴题难度较大,考查学生分析问题解决问题的能力,考查学生严谨的逻辑思维能力
已知 ,函数
,函数
(1)当 时,求函数
时,求函数 在点(1,
在点(1, )的切线方程;
)的切线方程;
(2)求函数 在[-1,1]的极值;
在[-1,1]的极值;
(3)若在 上至少存在一个实数x0,使
上至少存在一个实数x0,使 >g(xo)成立,求正实数
>g(xo)成立,求正实数 的取值范围。
的取值范围。
【解析】本试题中导数在研究函数中的运用。(1)中 ,那么当
,那么当 时,
时, 又
又  所以函数
所以函数 在点(1,
在点(1, )的切线方程为
)的切线方程为 ;(2)中令
;(2)中令 有
有 

对a分类讨论 ,和
,和 得到极值。(3)中,设
得到极值。(3)中,设 ,
, ,依题意,只需
,依题意,只需 那么可以解得。
那么可以解得。
解:(Ⅰ)∵ ∴
∴ 
∴ 当 时,
时, 又
又 
∴ 函数 在点(1,
在点(1, )的切线方程为
)的切线方程为 --------4分
--------4分
(Ⅱ)令 有
有 

①
当 即
即 时
时
|
|
(-1,0) |
0 |
(0, |
|
( |
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
极大值 |
|
极小值 |
|
故 的极大值是
的极大值是 ,极小值是
,极小值是
②
当 即
即 时,
时, 在(-1,0)上递增,在(0,1)上递减,则
在(-1,0)上递增,在(0,1)上递减,则 的极大值为
的极大值为 ,无极小值。
,无极小值。
综上所述  时,极大值为
时,极大值为 ,无极小值
,无极小值
 时 极大值是
时 极大值是 ,极小值是
,极小值是 ----------8分
----------8分
(Ⅲ)设 ,
,
对 求导,得
求导,得
∵ ,
,

∴  在区间
在区间 上为增函数,则
上为增函数,则
依题意,只需 ,即
,即
解得  或
或 (舍去)
(舍去)
则正实数 的取值范围是(
的取值范围是(
 ,
, )
)
设点 是抛物线
是抛物线

 的焦点,
的焦点, 是抛物线
是抛物线 上的
上的 个不同的点(
个不同的点(
 ).
).
(1) 当 时,试写出抛物线
时,试写出抛物线 上的三个定点
上的三个定点 、
、 、
、 的坐标,从而使得
的坐标,从而使得
 ;
;
(2)当 时,若
时,若 ,
,
求证: ;
;
(3) 当 时,某同学对(2)的逆命题,即:
时,某同学对(2)的逆命题,即:
“若 ,则
,则 .”
.”
开展了研究并发现其为假命题.
请你就此从以下三个研究方向中任选一个开展研究:
① 试构造一个说明该逆命题确实是假命题的反例(本研究方向最高得4分);
② 对任意给定的大于3的正整数 ,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);
,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);
③ 如果补充一个条件后能使该逆命题为真,请写出你认为需要补充的一个条件,并说明加上该条件后,能使该逆命题为真命题的理由(本研究方向最高得10分).
【评分说明】本小题若填空不止一个研究方向,则以实得分最高的一个研究方向的得分作为本小题的最终得分.
【解析】第一问利用抛物线 的焦点为
的焦点为 ,设
,设 ,
,
分别过 作抛物线
作抛物线 的准线
的准线 的垂线,垂足分别为
的垂线,垂足分别为 .
.
由抛物线定义得到
第二问设 ,分别过
,分别过 作抛物线
作抛物线 的准线
的准线 垂线,垂足分别为
垂线,垂足分别为 .
.
由抛物线定义得


第三问中①取 时,抛物线
时,抛物线 的焦点为
的焦点为 ,
,
设 ,
, 分别过
分别过
 作抛物线
作抛物线 的准线
的准线 垂线,垂足分别为
垂线,垂足分别为
 .由抛物线定义得
.由抛物线定义得




 ,
,
则 ,不妨取
,不妨取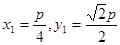 ;
;
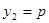 ;
;
 ;
;
解:(1)抛物线 的焦点为
的焦点为 ,设
,设 ,
,
分别过 作抛物线
作抛物线 的准线
的准线 的垂线,垂足分别为
的垂线,垂足分别为 .由抛物线定义得
.由抛物线定义得


因为 ,所以
,所以 ,
,
故可取

 满足条件.
满足条件.
(2)设 ,分别过
,分别过 作抛物线
作抛物线 的准线
的准线 垂线,垂足分别为
垂线,垂足分别为 .
.
由抛物线定义得


 又因为
又因为



 ;
;
所以

 .
.
(3) ①取 时,抛物线
时,抛物线 的焦点为
的焦点为 ,
,
设 ,
, 分别过
分别过
 作抛物线
作抛物线 的准线
的准线 垂线,垂足分别为
垂线,垂足分别为
 .由抛物线定义得
.由抛物线定义得




 ,
,
则 ,不妨取
,不妨取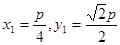 ;
;
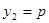 ;
;
 ;
; ,
,
则

 ,
,

 .
.
故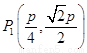 ,
, ,
, ,
, 是一个当
是一个当 时,该逆命题的一个反例.(反例不唯一)
时,该逆命题的一个反例.(反例不唯一)
② 设 ,分别过
,分别过 作
作
抛物线 的准线
的准线 的垂线,垂足分别为
的垂线,垂足分别为 ,
,
由 及抛物线的定义得
及抛物线的定义得
 ,即
,即 .
.
因为上述表达式与点 的纵坐标无关,所以只要将这
的纵坐标无关,所以只要将这 点都取在
点都取在 轴的上方,则它们的纵坐标都大于零,则
轴的上方,则它们的纵坐标都大于零,则






 ,
,
而 ,所以
,所以 .
.
(说明:本质上只需构造满足条件且 的一组
的一组 个不同的点,均为反例.)
个不同的点,均为反例.)
③ 补充条件1:“点 的纵坐标
的纵坐标 (
( )满足
)满足  ”,即:
”,即:
“当 时,若
时,若 ,且点
,且点 的纵坐标
的纵坐标 (
( )满足
)满足 ,则
,则 ”.此命题为真.事实上,设
”.此命题为真.事实上,设 ,
,
分别过 作抛物线
作抛物线 准线
准线 的垂线,垂足分别为
的垂线,垂足分别为 ,由
,由 ,
,
及抛物线的定义得 ,即
,即 ,则
,则






 ,
,
又由 ,所以
,所以 ,故命题为真.
,故命题为真.
补充条件2:“点 与点
与点
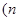 为偶数,
为偶数, 关于
关于 轴对称”,即:
轴对称”,即:
“当 时,若
时,若 ,且点
,且点 与点
与点
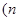 为偶数,
为偶数, 关于
关于 轴对称,则
轴对称,则 ”.此命题为真.(证略)
”.此命题为真.(证略)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com