
题目列表(包括答案和解析)
已知函数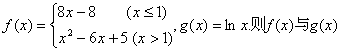 两函数的图像的交点个数为
(
)
两函数的图像的交点个数为
(
)
A.1 B.2 C.3 D.4
已知直线![]() 与函数
与函数![]() 的图像的两个相邻交点之间的距离为
的图像的两个相邻交点之间的距离为![]() 。
。
(I)求![]() 的解析式,并求出
的解析式,并求出![]()
![]() 的单调递增区间;
的单调递增区间;
(II)将函数![]() 的图像向左平移
的图像向左平移![]() 个单位得到函数
个单位得到函数![]() 的图像,求函数
的图像,求函数![]() 的最大值及
的最大值及![]() 取得最大值时x的取值集合。
取得最大值时x的取值集合。
已知直线 与函数
与函数 的图像的两个相邻交点之间的距离为
的图像的两个相邻交点之间的距离为 。
。
(I)求 的解析式,并求出
的解析式,并求出 的单调递增区间
的单调递增区间
(II)将函数 的图像向左平移
的图像向左平移 个单位得到函数
个单位得到函数 的图像,求函数
的图像,求函数 的最大值及
的最大值及 取得最大值时x的取值集合。
取得最大值时x的取值集合。
已知直线 与函数
与函数 的图像的两个相邻交点之间的距离为
的图像的两个相邻交点之间的距离为 。
。
(I)求 的解析式,并求出
的解析式,并求出 的单调递增区间
的单调递增区间
(II)将函数 的图像向左平移
的图像向左平移 个单位得到函数
个单位得到函数 的图像,求函数
的图像,求函数 的最大值及
的最大值及 取得最大值时x的取值集合。
取得最大值时x的取值集合。
已知直线![]() 与函数
与函数![]() 的图像的两个相邻交点之间的距离为
的图像的两个相邻交点之间的距离为![]() 。
。
(I)求![]() 的解析式,并求出
的解析式,并求出![]() 的单调递增区间;
的单调递增区间;
(II)将函数![]() 的图像向左平移
的图像向左平移![]() 个单位得到函数
个单位得到函数![]() 的图像,求函数
的图像,求函数![]() 的最大值及
的最大值及![]() 取得最大值时x的取值集合。
取得最大值时x的取值集合。
一、选择题:本大题共12小题,每小题5分,共60分。
1―5 DBCDC 6―10BBCAB 11―12 DB
二、填空题:本大题共4小题,每小题4分,共16分。
13.“ ” 14.
” 14. 15.1200 16.
15.1200 16.
三、解答题:本大题共6小题,共80分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分13分)
解:(I)由已知

(II)

|