
题目列表(包括答案和解析)
(04年天津卷理)(12分)
已知定义在R上的函数![]() 和数列
和数列![]() 满足下列条件:
满足下列条件:
![]() ,
,
![]()
其中![]() 为常数,
为常数,![]() 为非零常数。
为非零常数。
(I)令![]() ,证明数列
,证明数列![]() 是等比数列;
是等比数列;
(II)求数列![]() 的通项公式;
的通项公式;
(III)当![]() 时,求
时,求![]()
(本小题满分13分)
品酒师需定期接受酒味鉴别功能测试,一种通常采用的测试方法如下:拿出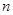 瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这
瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这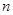 瓶酒,并重新按品质优劣为它们排序,这称为一轮测试。根据一轮测试中的两次排序的偏离程度的高低为其评为。
瓶酒,并重新按品质优劣为它们排序,这称为一轮测试。根据一轮测试中的两次排序的偏离程度的高低为其评为。
现设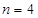 ,分别以
,分别以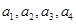 表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令
表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令
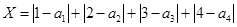 ,
,
则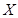 是对两次排序的偏离程度的一种描述。
是对两次排序的偏离程度的一种描述。
(Ⅰ)写出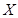 的可能值集合;
的可能值集合;
(Ⅱ)假设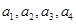 等可能地为1,2,3,4的各种排列,求
等可能地为1,2,3,4的各种排列,求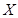 的分布列;
的分布列;
(Ⅲ)某品酒师在相继进行的三轮测试中,都有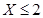 ,
,
(i)试按(Ⅱ)中的结果,计算出现这种现象的概率(假定各轮测试相互独立);
(ii)你认为该品酒师的酒味鉴别功能如何?说明理由。
(本小题满分13分)
品酒师需定期接受酒味鉴别功能测试,一种通常采用的测试方法如下:拿出 瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这
瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这 瓶酒,并重新按品质优劣为它们排序,这称为一轮测试。根据一轮测试中的两次排序的偏离程度的高低为其评为。
瓶酒,并重新按品质优劣为它们排序,这称为一轮测试。根据一轮测试中的两次排序的偏离程度的高低为其评为。
现设 ,分别以
,分别以 表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令
表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令
 ,
,
则 是对两次排序的偏离程度的一种描述。
是对两次排序的偏离程度的一种描述。
(Ⅰ)写出 的可能值集合;
的可能值集合;
(Ⅱ)假设 等可能地为1,2,3,4的各种排列,求
等可能地为1,2,3,4的各种排列,求 的分布列;
的分布列;
(Ⅲ)某品酒师在相继进行的三轮测试中,都有 ,
,
(i)试按(Ⅱ)中的结果,计算出现这种现象的概率(假定各轮测试相互独立);
(ii)你认为该品酒师的酒味鉴别功能如何?说明理由。
(本小题满分13分)
品酒师需定期接受酒味鉴别功能测试,一种通常采用的测试方法如下:拿出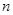 瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这
瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这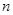 瓶酒,并重新按品质优劣为它们排序,这称为一轮测试。根据一轮测试中的两次排序的偏离程度的高低为其评为。
瓶酒,并重新按品质优劣为它们排序,这称为一轮测试。根据一轮测试中的两次排序的偏离程度的高低为其评为。
现设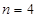 ,分别以
,分别以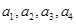 表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令
表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令
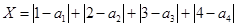 ,
,
则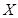 是对两次排序的偏离程度的一种描述。
是对两次排序的偏离程度的一种描述。
(Ⅰ)写出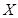 的可能值集合;
的可能值集合;
(Ⅱ)假设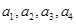 等可能地为1,2,3,4的各种排列,求
等可能地为1,2,3,4的各种排列,求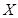 的分布列;
的分布列;
(Ⅲ)某品酒师在相继进行的三轮测试中,都有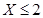 ,
,
(i)试按(Ⅱ)中的结果,计算出现这种现象的概率(假定各轮测试相互独立);
(ii)你认为该品酒师的酒味鉴别功能如何?说明理由。
(本小题满分13分)
品酒师需定期接受酒味鉴别功能测试,一种通常采用的测试方法如下:拿出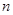 瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这
瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这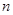 瓶酒,并重新按品质优劣为它们排序,这称为一轮测试。根据一轮测试中的两次排序的偏离程度的高低为其评为。
瓶酒,并重新按品质优劣为它们排序,这称为一轮测试。根据一轮测试中的两次排序的偏离程度的高低为其评为。
现设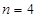 ,分别以
,分别以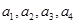 表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令
表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令
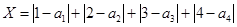 ,
,
则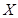 是对两次排序的偏离程度的一种描述。
是对两次排序的偏离程度的一种描述。
(Ⅰ)写出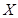 的可能值集合;
的可能值集合;
(Ⅱ)假设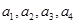 等可能地为1,2,3,4的各种排列,求
等可能地为1,2,3,4的各种排列,求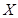 的分布列;
的分布列;
(Ⅲ)某品酒师在相继进行的三轮测试中,都有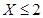 ,
,
(i)试按(Ⅱ)中的结果,计算出现这种现象的概率(假定各轮测试相互独立);
(ii)你认为该品酒师的酒味鉴别功能如何?说明理由。
一、选择题:本大题共12小题,每小题5分,共60分。
1―5 DBCDC 6―10BBCAB 11―12 DB
二、填空题:本大题共4小题,每小题4分,共16分。
13.“ ” 14.
” 14. 15.1200 16.
15.1200 16.
三、解答题:本大题共6小题,共80分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分13分)
解:(I)由已知

(II)

|