练习册

  • 练习册
  • 试题
    (II)若切线有且只有一个公共点.求实数a的值. 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题满分14分

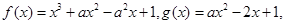    函数实数．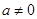

    （I）若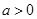，求函数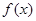的单调区间；

    （II）当函数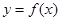与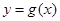的图象只有一个公共点且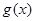存在最小值时，记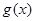的最小值为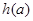，求的值域；

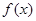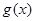    （III）若与在区间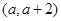内均为增函数，求的取值范围。

    （文）已知函数 ．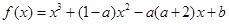

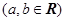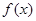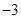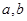     （I）若函数的图象过原点，且在原点处的切线斜率是，求的值；

     （II）若函数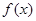在区间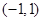上不单调，求的取值范围

     

    查看答案和解析>>

     

    一、选择题：本大题共12小题，每小题5分，共60分。

    1―5 DBCDC    6―10BBCAB    11―12 DB

    二、填空题：本大题共4小题，每小题4分，共16分。

    13．“”   14．    15．1200    16．

    三、解答题：本大题共6小题，共80分。解答应写出文字说明、证明过程或演算步骤。

    17．（本小题满分13分）

    解：（I）由已知

       （II）

    ∵面ABCD是正方形，∴点F为AC中点，……2分

    又∵点E是棱CC1中点，∴EF//AC1  …………4分

    又∵EF面EDB，AC1面EDB；

    ∴AC1⊥平面BDE  ………………5分

       （II）连结B1D、B1E

    长方体ABCD―A1B1C1D1中，DC⊥面BB1C1C

    所以在三棱锥D―BB1E中，

    19．解：（I）由条件得：   …………2分

        ………………4分

       ………………6分

       （II）由（I）得  …………8分

       

    20．解：（I）掷一枚硬币三次，列出所有可能情况共8种：

       （上上上），（上上下），（上下上），（上下下），（下上上），（下上下），（下下上），（下下下）；

        其中甲得2分、乙得1分的有3种，故所求概率  …………3分

       （II）在题设条件下，至多还要2局，情形一：在第四局，硬币正面朝上，则甲积3分、乙积1分，甲获胜，概率为1/2；情形二：在第四局，硬币正面朝下，第五局硬币正面朝上，则甲积3分、乙积2分，甲获胜，概率为1/4。由加法公式，甲获胜的概率为1/2+1/4=3/4。   ………………8分

    21．解：（I）∵F1，F2三等份BD， …………1分

           ………………3分

       （II）由（I）知为BF2的中点，

       

       （III）依题意直线AC的斜率存在，

       

       

       （III）解法二 依题意直线AC的斜率存在，

       

       

       （III）[解法二]同理

    20．（I）解：

      

       （II）切线l与曲线有且只有一个公共点等价

    ①

    的唯一解；  ………………10分

    ②

    x

    （―∞，0）

    ―1

    +

    0

    ―

    0

    +

    极大值0

    极小值

    ③

    x

    ―1

    +

    0

    ―

    0

    +

    极大值

    极小值0

     


    同步练习册答案