
(I)证明:(1)连接CD1
∵四棱柱ABCD―A1B1C1D1中,底面ABCD是菱形
∴A1D1//AD,AD//BC,A1D1=AD,AD=BC;
∴A1D1//BC,A1D1=BC,
∴四边形A1BCD1为平行四边形;∴A1B//D1C………3分
∵点E、F分别是棱CC1、C1D1的中点;∴EF//D1C
又∴EF//A1B
又∵A1B 平面A1DB,EF
平面A1DB,EF 面A1DB;
面A1DB;
∴EF⊥平面A1BD ………………6分
(II)连结AC交BD于点G,连接A1G,EG
∵四棱柱ABCD―A1B1C1D1中,A1A⊥底面ABCD,
底面ABCD是菱形
∴AA1⊥AB,AA1⊥AD,EC⊥BC,EC⊥DC,
AD=AB,BC=CD
∵底面ABCD是菱形,∴点G为BD中点,
∴A1G⊥BD,EG⊥BD
∴∠A1GE为直二面角A1―BD―E的平面角,
∴∠A1GE=90°………………3分
在棱形ABCD中,∠DAB=60°,AB=2,
∴∠ABC=120°,
∴AC=
∴AG=GC= ………………10分
………………10分
在面ACC1A1中,△AGA1,△GCE为直角三角形
∵∠A1GE=90°∴∠EGC+∠A1GA=90°,∴∠EGC=∠AA1G,
∴Rt△A1AG∽Rt△ECG ………………12分

解法二:
(I)证明:取AB的中点G,连接GD
∵底面ABCD是菱形,∠DAB=60°,AB=2
∴△ABD是正三角形,∴DG⊥AB,DG=
又∵AB//CD,∴DG⊥DC …………2分
∵四棱柱ABCD―A1B1C1D1为直四棱柱,AA1//DD1
A1A⊥底面ABCD,∴DD1⊥底面ABCD
以D为坐标原点,射线DG为x轴的正半轴,射线DC为y轴的正半轴,
建立如图所示空间直角坐标系D―xyz.



18.解:(I)掷一枚硬币三次,列出所有可能情况共8种: (上上上),(上上下),(上下上),(上下下),(下上上),(下上下),(下下上),(下下下); 其中甲得2分、乙得1分的有3种,故所求概率 …………3分 …………3分 (II)在题设条件下,至多还要2局,情形一:在第四局,硬币正面朝上,则甲积3分、乙积1分,甲获胜,概率为1/2;情形二:在第四局,硬币正面朝下,第五局硬币正面朝上,则甲积3分、乙积2分,甲获胜,概率为1/4。由加法公式,甲获胜的概率为1/2+1/4=3/4。 ………………8分 (III)据题意,ξ的取值为3、4、5, 且 ………………11分 ………………11分  其分布列如下: ξ 3 4 5 P 1/4 3/8 3/8  ………………13分 ………………13分 19.解:(I)∵F1,F2三等份BD, …………1分 …………1分  ………………3分 ………………3分 (II)由(I)知 为BF2的中点, 为BF2的中点,  (III)依题意直线AC的斜率存在,

同理可求  (III)法二: 
 
20.(I)解: 
(II)切线l与曲线 有且只有一个公共点等价 有且只有一个公共点等价 
①  的唯一解; ………………7分 的唯一解; ………………7分
② x (―1,0) 0 



+ 0 ― 0 + 

极大值0 
极小值 

③ x 


0 

+ 0 ― 0 + 

极大值 
极小值0 

(III) 
21.(I)由已知BA= ………………2分 ………………2分 任取曲线 
则有 = = ,即有 ,即有 ………………5分 ………………5分  ………………6分 ………………6分
即 …………① 与 …………① 与 ………………② ………………② 比较①②得 (II)设圆C上的任意一点的极坐标 ,过OC的直径的另一端点为B, ,过OC的直径的另一端点为B, 边PO,PB则在直角三角形OPB中, …………5分 …………5分 (写 不扣分) 不扣分) 从而有 ………………7分 ………………7分 (III)证: 为定值, 为定值, 利用柯西不等式得到  ………5分 ………5分

| | | |

 和直线
和直线 ,
, 的直角坐标方程;(2)当
的直角坐标方程;(2)当 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.
 和
和 ,不等式
,不等式 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.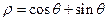 和直线
和直线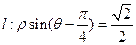 ,
, 的直角坐标方程;(2)当
的直角坐标方程;(2)当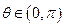 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.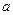
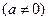 和
和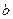 ,不等式
,不等式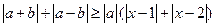 恒成立,试求实数
恒成立,试求实数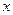 的取值范围.
的取值范围.![]() =
=![]() =
=![]() -ab,所以ab≤
-ab,所以ab≤![]() ,故B错;
,故B错;![]() +
+![]() =
=![]() =
=![]() ≥4,故A错;由基本不等式得
≥4,故A错;由基本不等式得![]() ≤
≤![]() =
=![]() ,即
,即![]() +
+![]() ≤
≤![]() ,故C正确;a2+b2=(a+b)2-2ab=1-2ab≥1-2×
,故C正确;a2+b2=(a+b)2-2ab=1-2ab≥1-2×![]() =
=![]() ,故D错.故选C.
,故D错.故选C. 满足
满足 ,且当
,且当 时,
时, ,则当
,则当 时,
时, 的最小值为( )
的最小值为( ) (B)
(B) (C)
(C) (D)
(D)
 作圆
作圆 的弦,其中弦长为整数的共有 ( )
的弦,其中弦长为整数的共有 ( ) 


