
题目列表(包括答案和解析)
已知a、b、c成等比数列,如果a、x、b和b、y、c都成等差数列,则![]() =_________
=_________![]()
已知a、b、c成等比数列,如果a、x、b和b、y、c都成等差数列,则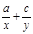 =_________.
=_________.
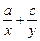 =_________
=_________
已知![]() a、b、c成等比数列,如果a、x、b和b、y、c都成等差数列,则
a、b、c成等比数列,如果a、x、b和b、y、c都成等差数列,则![]() =____
=____
已知a、b、c成等比数列,如果a、x、b和b、y、c都成等差数列,则![]() =_________.
=_________.
难点磁场
 解法一:将Sm=30,S
解法一:将Sm=30,S d,得:
d,得:
解法二:由 知,要求S
知,要求S ],将②-①得ma1+
],将②-①得ma1+  d=70,∴S
d=70,∴S
解法三:由等差数列{an}的前n项和公式知,Sn是关于n的二次函数,即Sn=An2+Bn(A、B是常数).将Sm=30,S
解法四:S
解法五:根据等差数列性质知:Sm,S
∴S
∴点(n,  )是直线y=
)是直线y= +a1上的一串点,由三点(m,
+a1上的一串点,由三点(m, ),(
),( ),(
),( )共线,易得S
)共线,易得S
解法七:令m=1得S1=30,S2=100,得a1=30,a1+a2=100,∴a1=30,a2=70
∴a3=70+(70-30)=110
∴S3=a1+a2+a3=210
答案:210
歼灭难点训练
一、1.解析:利用等比数列和的性质.依题意, ,而a1=-1,故q≠1,
,而a1=-1,故q≠1,
∴ ,根据等比数列性质知S5,S10-S5,S15-S10,…,也成等比数列,且它的公比为q5,∴q5=-
,根据等比数列性质知S5,S10-S5,S15-S10,…,也成等比数列,且它的公比为q5,∴q5=- ,即q=-
,即q=- .
.
答案:B
二、2.解析:解出a、b,解对数不等式即可.
答案:(-∞,8)
答案:第11项a11=29
4.解法一:赋值法.
解法二:
b=aq,c=aq2,x= (a+b)=
(a+b)= a(1+q),y=
a(1+q),y= (b+c)=
(b+c)= aq(1+q),
aq(1+q),
答案:2
(2)解法一:由d<0可知a1>a2>a3>…>a12>a13,因此,在S1,S2,…,S12中Sk为最大值的条件为:ak≥0且ak+1<0,即
因为k是正整数,所以k=6,即在S1,S2,…,S12中,S6最大.
解法二:由d<0得a1>a2>…>a12>a13,因此,若在1≤k≤12中有自然数k,使得ak≥0,且ak+1<0,则Sk是S1,S2,…,S12中的最大值.由等差数列性质得,当m、n、p、q∈N*,且m+n=p+q时,am+an=ap+aq.所以有: S13<0,∴a7<0,a7+a6=a1+a12=
S13<0,∴a7<0,a7+a6=a1+a12= S12>0,∴a6≥-a7>0,故在S1,S2,…,S12中S6最大.
S12>0,∴a6≥-a7>0,故在S1,S2,…,S12中S6最大.
∵- <d<-3,∴6<
<d<-3,∴6< (5-
(5- )<6.5.从而,在正整数中,当n=6时,[n-
)<6.5.从而,在正整数中,当n=6时,[n- (5-
(5- )]2最小,所以S6最大.
)]2最小,所以S6最大.
点评:该题的第(1)问通过建立不等式组求解属基本要求,难度不高,入手容易.第(2)问难度较高,为求{Sn}中的最大值Sk,1≤k≤12,思路之一是知道Sk为最大值的充要条件是ak≥0且ak+1<0,思路之三是可视Sn为n的二次函数,借助配方法可求解.它考查了等价转化的数学思想、逻辑思维能力和计算能力,较好地体现了高考试题注重能力考查的特点.而思路之二则是通过等差数列的性质等和性探寻数列的分布规律,找出“分水岭”,从而得解.
6.解:(1)由题意知a52=a1?a17,即(a1+4d)2=a1(a1+16d) a1d=2d2,
a1d=2d2,
由①②得a1?3n-1= ?a1.∵a1=2d≠0,∴bn=2?3n-1-1.
?a1.∵a1=2d≠0,∴bn=2?3n-1-1.
(2)Tn=C b1+C
b1+C b2+…+C
b2+…+C bn=C
bn=C (2?30-1)+C
(2?30-1)+C ?(2?31-1)+…+C
?(2?31-1)+…+C (2?3n-1-1)=
(2?3n-1-1)= (C
(C +C
+C ?32+…+C
?32+…+C ?3n)-(C
?3n)-(C +C
+C +…+C
+…+C )=
)= [(1+3)n-1]-(2n-1)=
[(1+3)n-1]-(2n-1)=  ?4n-2n+
?4n-2n+ ,
,
7.解:∵{an}为等差数列,{bn}为等比数列,∴a2+a4=
已知a2+a4=b3,b2?b4=a3,∴b3=
8.证明:(1)∵{an}是等差数列,∴2ak+1=ak+ak+2,故方程akx2+2ak+1x+ak+2=0可变为(akx+ak+2)(x+1)=0,
∴当k取不同自然数时,原方程有一个公共根-1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com