
题目列表(包括答案和解析)
已知点的序列An(xn,0),n∈N,其中x1=0,x2=a(a>0),A3是线段A1A2的中点,A4是线段A2A3的中点,…,An是线段An-2An-1的中点,….
(1)写出xn与xn-1、xn-2之间关系式(n≥3);
(2)设an=xn+1-xn,计算a1,a2,a3,由此推测数列{an}的通项公式,并加以证明;
(3)求![]() xn
xn
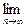 xn
xn已知点的序列An(xn,0)(n∈N+),其中x1=0,x2=a(a>0),A3是线段A1A2的中点,A4是线段A2A3的中点,……An是线段![]() 的中点,…….已知an=xn+1-xn,试写出数列{an}的通项公式.
的中点,…….已知an=xn+1-xn,试写出数列{an}的通项公式.
已知点的序列An(xn,0),x∈N,其中x1=0,x2=a(a>0),A3是线段A1A2的中点,A4是线段A2A3的中点,…,An是线段An-2An-1的中点,…
(1)写出xn与xn-1、xn-2之间的关系(n≥3);
(2)设an=xn+1-xn,计算a1,a2,a3,由此推测数列{an}的通项公式,并加以证明
(3)求![]() xn
xn
已知点的序列An(xn,0),n∈N+,其中x1=0,x2=a(a>0),A3是线段A1A2的中点,A4是线段A2A3的中点,…,An是线段![]() 的中点,……
的中点,……
(1)写出xn与x![]() 、x
、x![]() 之间的关系式(n≥3);
之间的关系式(n≥3);
(2)设an=xn+1-xn,计算a1,a2,a3,由此推测数列{an}的通项公式.
难点磁场
解:(1)设f(x)=a(x- )2-
)2- ,由f(1)=0得a=1.
,由f(1)=0得a=1.
∴f(x)=x2-(t+2)x+t+1.
(2)将f(x)=(x-1)[x-(t+1)]代入已知得:
(x-1)[x-(t+1)]g(x)+anx+bn=xn+1,上式对任意的x∈R都成立,取x=1和x=t+1分别代入上式得:
 且t≠0,解得an=
且t≠0,解得an= [(t+1)n+1-1],bn=
[(t+1)n+1-1],bn= [1-(t+1
[1-(t+1 n)
n)
(3)由于圆的方程为(x-an)2+(y-bn)2=rn2,又由(2)知an+bn=1,故圆Cn的圆心On在直线x+y=1上,又圆Cn与圆Cn+1相切,故有rn+rn+1= |an+1-an|=
|an+1-an|= (t+1)n+1?
(t+1)n+1?
∴Sn=π(r12+r22+…+rn2)= [(t+1)2n-1]
[(t+1)2n-1]
歼灭难点训练
一、1.解析:当a=n时y=n(n+1)x2-(2n+1)x+1
答案:A
二、2.解析:由1,x1,x2,4依次成等差数列得:2x1=x2+1,x1+x2=5解得x1=2,x2=3.又由1,y1,y2,8依次成等比数列,得y12=y2,y1y2=8,解得y1=2,y2=4,
答案:1
3.解析:第一次容器中有纯酒精a-b即a(1- )升,第二次有纯酒精a(1-
)升,第二次有纯酒精a(1- )-
)- ,即a(1-
,即a(1- )2升,故第n次有纯酒精a(1-
)2升,故第n次有纯酒精a(1- )n升.
)n升.
4.解析:从2001年到2005年每年的国内生产总值构成以95933为首项,以7.3%为公比的等比数列,∴a5=95933(1+7.3%)4≈120000(亿元).
答案:120000
三、
5.解:(1)由题意得rqn-1+rqn>rqn+1.由题设r>0,q>0,故从上式可得:q2-q-1<0,解得 <q<
<q< ,因q>0,故0<q<
,因q>0,故0<q< ;
;
(2)∵ .b1=1+r≠0,所以{bn}是首项为1+r,公比为q的等比数列,从而bn=(1+r)qn-1.
.b1=1+r≠0,所以{bn}是首项为1+r,公比为q的等比数列,从而bn=(1+r)qn-1.
当q=1时,Sn=n(1+r),
 ,从上式可知,当n-20.2>0,即n≥21(n∈N*)时,Cn随n的增大而减小,故
,从上式可知,当n-20.2>0,即n≥21(n∈N*)时,Cn随n的增大而减小,故
当n-20.2<0,即n≤20(n∈N*)时,Cn也随n的增大而减小,故1>Cn≥C20=1+ =-4 ②
=-4 ②
综合①②两式知,对任意的自然数n有C20≤Cn≤C21,故{Cn}的最大项C21=2.25,最小项C20=-4.
6.解:(1)第1位职工的奖金a1= ,第2位职工的奖金a2=
,第2位职工的奖金a2= (1-
(1- )b,第3位职工的奖金a3=
)b,第3位职工的奖金a3= (1-
(1- )2b,…,第k位职工的奖金ak=
)2b,…,第k位职工的奖金ak= (1-
(1- )k-1b;
)k-1b;
(2)ak-ak+1= (1-
(1- )k-1b>0,此奖金分配方案体现了“按劳分配”或“不吃大锅饭”的原则.
)k-1b>0,此奖金分配方案体现了“按劳分配”或“不吃大锅饭”的原则.
(3)设fk(b)表示奖金发给第k位职工后所剩余数,则f1(b)=(1- )b,f2(b)=(1-
)b,f2(b)=(1- )2b,…,fk(b)=(1-
)2b,…,fk(b)=(1- )kb.得Pn(b)=fn(b)=(1-
)kb.得Pn(b)=fn(b)=(1- )nb,
)nb,
7.解:设an表示第n年的废旧物资回收量,Sn表示前n年废旧物资回收总量,则数列{an}是以10为首项,1+20%为公比的等比数列.
(1)a6=10(1+20%)5=10×1.25=24.8832≈25(万吨)
∴从1996年到2000年共节约开采矿石20×99.3≈1986(万吨)
(3)由于从1996年到2001年共减少工业废弃垃圾4×99.3=397.2(万吨),
∴从1996年到2001年共节约:
证法一:因为a1=a>0,且
证法二:用数学归纳法证明:
(?)当n=1时,a1=x2-x1=a=(- )0a,公式成立;
)0a,公式成立;
(?)假设当n=k时,公式成立,即ak=(- )k-1a成立.
)k-1a成立.
那么当n=k+1时,
据(?)(?)可知,对任意n∈N,公式an=(- )n-1a成立.
)n-1a成立.
(3)当n≥3时,有xn=(xn-xn-1)+(xn-1-xn-2)+…+(x2-x1)+x1
=an-1+an-2+…+a1,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com