
题目列表(包括答案和解析)
已知cosα+sinβ=![]() ,sinα+cosβ的取值范围是D,x∈D,求函数y=
,sinα+cosβ的取值范围是D,x∈D,求函数y=![]() 的最小值,并求取得最小值时x的值.
的最小值,并求取得最小值时x的值.
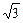 ,sinα+cosβ的取值范围是D,x∈D,求函数y=
,sinα+cosβ的取值范围是D,x∈D,求函数y= 的最小值,并求取得最小值时x的值.
的最小值,并求取得最小值时x的值.| OB |
| OC |
|
| OA |
| OB |
A、[
| ||||
B、[-
| ||||
C、[-1,
| ||||
D、[-1,-
|
| a |
| b |
| 3 |
| a |
| b |
| A、[-1,2] | ||
| B、[-1,1] | ||
| C、[-2,2] | ||
D、[-
|
| A、(-2,3) | B、[-2,3) | C、(-2,3] | D、[-2,3] |
难点磁场
∴sin2α=sin[(α-β)+(α+β)]
=sin(α-β)cos(α+β)+cos(α-β)sin(α+β)
∴sin2α+sin2β=2sin(α+β)cos(α-β)=-
sin2α-sin2β=2cos(α+β)sin(α-β)=-
歼灭难点训练
一、1.解析:∵a>1,tanα+tanβ=-
tanα+tanβ= ,
, )∴α、β∈(-
)∴α、β∈(- ,θ),则
,θ),则 ∈(-
∈(- ,0),又tan(α+β)=
,0),又tan(α+β)= ,
,
答案:B
三、4.答案:2
7.解:以OA为x轴.O为原点,建立平面直角坐标系,并设P的坐标为(cosθ,sinθ),则
|PS|=sinθ.直线OB的方程为y= x,直线PQ的方程为y=sinθ.联立解之得Q(
x,直线PQ的方程为y=sinθ.联立解之得Q( sinθ;sinθ),所以|PQ|=cosθ-
sinθ;sinθ),所以|PQ|=cosθ- sinθ.
sinθ.
于是SPQRS=sinθ(cosθ- sinθ)=
sinθ)= (
( sinθcosθ-sin2θ)=
sinθcosθ-sin2θ)= (
( sin2θ-
sin2θ- )=
)= (
( sin2θ+
sin2θ+ cos2θ-
cos2θ- )=
)=  sin(2θ+
sin(2θ+ )-
)- .
.
∴sin(2θ+ )=1时,PQRS面积最大,且最大面积是
)=1时,PQRS面积最大,且最大面积是 ,此时,θ=
,此时,θ= ,点P为
,点P为 的中点,P(
的中点,P( ).
).
8.解:设u=sinα+cosβ.则u2+( )2=(sinα+cosβ)2+(cosα+sinβ)2=2+2sin(α+β)≤4.∴u2≤1,-1≤u≤1.即D=[-1,1],设t=
)2=(sinα+cosβ)2+(cosα+sinβ)2=2+2sin(α+β)≤4.∴u2≤1,-1≤u≤1.即D=[-1,1],设t= ,∵-1≤x≤1,∴1≤t≤
,∵-1≤x≤1,∴1≤t≤ .x=
.x= .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com