
题目列表(包括答案和解析)
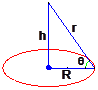
如右图,在半径为R的圆桌的正中央上空挂一盏电灯,桌子边缘一点处的照度和灯光射到桌子边缘的光线与桌面的夹角θ的正弦成正比,角和这一点到光源的距离 r的平方成反比,即I=k·![]() ,其中 k是一个和灯光强度有关的常数,那么怎样选择电灯悬挂的高度h,才能使桌子边缘处最亮?
,其中 k是一个和灯光强度有关的常数,那么怎样选择电灯悬挂的高度h,才能使桌子边缘处最亮?
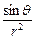 ,其中k是一个和灯光强度有关的常数,那么怎样选择电灯悬挂的高度h,才能使桌子边缘处最亮?
,其中k是一个和灯光强度有关的常数,那么怎样选择电灯悬挂的高度h,才能使桌子边缘处最亮?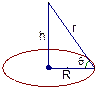
难点磁场
解法一:由题设条件知B=60°,A+C=120°.
设α= ,则A-C=2α,可得A=60°+α,C=60°-α,
,则A-C=2α,可得A=60°+α,C=60°-α,
(2cosα- )(2
)(2 cosα+3)=0,∵2
cosα+3)=0,∵2 cosα+3≠0,
cosα+3≠0,
解法二:由题设条件知B=60°,A+C=120°
 ①,把①式化为cosA+cosC=-2
①,把①式化为cosA+cosC=-2 cosAcosC ②,
cosAcosC ②,
利用和差化积及积化和差公式,②式可化为
将cos(A-C)=2cos2( )-1代入
④:4
)-1代入
④:4 cos2(
cos2( )+2cos
)+2cos -3
-3 =0,(*),
=0,(*),
歼灭难点训练
一、1.解析:其中(3)(4)正确.
答案: B
二、2.解析:∵A+B+C=π,A+C=2B,
3.解析:∵A为最小角∴
∵cos(B+C)=-cosA=-cos[( ,
,
三、4.解:如图:连结BD,则有四边形ABCD的面积:
S=S△ABD+S△CDB= ?AB?ADsinA+
?AB?ADsinA+ ?BC?CD?sinC
?BC?CD?sinC
∵A+C=180°,∴sinA=sinC
故S= (AB?AD+BC?CD)sinA=
(AB?AD+BC?CD)sinA= (2×4+6×4)sinA=16sinA
(2×4+6×4)sinA=16sinA
由余弦定理,在△ABD中,BD2=AB2+AD2-2AB?AD?cosA=20-16cosA
在△CDB中,BD2=CB2+CD2-2CB?CD?cosC=52-48cosC
∴20-16cosA=52-48cosC,∵cosC=-cosA,
∴64cosA=-32,cosA=- ,又0°<A<180°,∴A=120°故S=16sin120°=8
,又0°<A<180°,∴A=120°故S=16sin120°=8 .
.
7.解:由a、b、
∴sin2B=3sinC?sinA=3(- )[cos(A+C)-cos(A-C)]
)[cos(A+C)-cos(A-C)]
∵B=π-(A+C).∴sin2(A+C)=- [cos(A+C)-cos
[cos(A+C)-cos ]
]
即1-cos2(A+C)=- cos(A+C),解得cos(A+C)=-
cos(A+C),解得cos(A+C)=- .
.
∵0<A+C<π,∴A+C= π.又A-C=
π.又A-C= ∴A=
∴A= π,B=
π,B= ,C=
,C= .
.
8.解:按题意,设折叠后A点落在边BC上改称P点,显然A、P两点关于折线DE对称,又设∠BAP=θ,∴∠DPA=θ,∠BDP=2θ,再设AB=a,AD=x,∴DP=x.在△ABC中,
∠APB=180°-∠ABP-∠BAP=120°-θ,?
∵0°≤θ≤60°,∴60°≤60°+2θ≤180°,∴当60°+2θ=90°,即θ=15°时,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com